Modulus of an elliptic integral

The parameter which enters into the expression of the elliptic integral in Legendre normal form. For example, in the incomplete elliptic integral of the first kind,

(*)

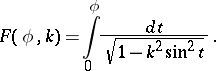The number is sometimes called the Legendre modulus, is called the complementary modulus. In applications the normal case usually holds; here the sharp angle for which is called the modular angle. The modulus also enters into the expression of the Jacobi elliptic functions, which arise from the inversion of elliptic integrals of the form (*).

References

[a1]	F. Bowman, "Introduction to elliptic functions with applications" , Dover, reprint (1961)