Schur ring
A certain kind of subring of the group algebra 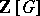 of a group
of a group 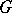 .
.
Let  be a finite group and
be a finite group and  a partition of
a partition of  . For each
. For each  , let
, let 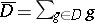 and
and  . Suppose that for each
. Suppose that for each  ,
, 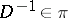 , and for all
, and for all 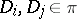 ,
, 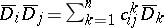 for certain
for certain 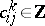 . Then the
. Then the  form the basis (over
form the basis (over 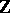 ) of a subring of
) of a subring of 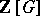 . These subrings are called Schur rings. A unitary Schur ring is one which contains the unit element of
. These subrings are called Schur rings. A unitary Schur ring is one which contains the unit element of 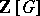 .
.
A subring 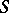 of
of 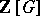 is a Schur ring over
is a Schur ring over  if and only if
if and only if  for all
for all 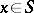 (where
(where 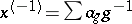 if
if 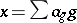 ) and it is closed under the Hadamard product
) and it is closed under the Hadamard product 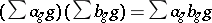 .
.
A symmetric Schur ring 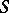 is a Schur ring for which
is a Schur ring for which 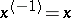 for all
for all 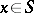 .
.
Historically, Schur rings were first studied by I. Schur [a1] and H. Wielandt [a2], who coined the name, in connection with the study of permutation groups; cf. [a3]–[a5] for applications of Schur rings to group theory. More recently it was discovered that they are also related to certain combinatorial structures, such as association schemes and strongly regular graphs, [a6], [a7].
References
| [a1] | I. Schur, "Zur Theorie der einfach transitiven Permutationsgruppen" Sitzungsber. Preuss. Akad. Wissenschaft. Berlin. Phys.-Math. Kl. (1933) pp. 598–623 |
| [a2] | H. Wielandt, "Zur Theorie der einfach transitiven Permutationsgruppen II" Math. Z. , 52 (1949) pp. 384–393 |
| [a3] | O. Tamaschke, "Schur-Ringe" , B.I. Wissenschaftsverlag Mannheim (1970) |
| [a4] | W.R. Scott, "Group theory" , Prentice-Hall (1964) |
| [a5] | H. Wielandt, "Finite permutation groups" , Acad. Press (1964) (Translated from German) |
| [a6] | E. Bannai, T. Ito, "Algebraic combinatorics I: Association schemes" , Benjamin/Cummings (1984) |
| [a7] | S.L. Ma, "On association schemes, Schur rings, strongly regular graphs and partial difference sets" Ars Comb. , 27 (1989) pp. 211–220 |
Schur ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schur_ring&oldid=15134