Pentaspherical coordinates

A kind of homogeneous coordinates 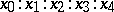for a point 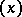in complex inversive space. The numbers 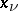, not all zero, are connected by the relation

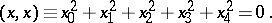All points 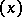which satisfy a linear equation

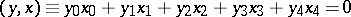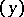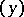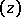are said to form a sphere, with coordinates . Two spheres and are orthogonal if 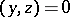, tangent if

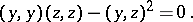If two spheres 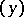and 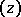intersect, the expression

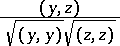measures the cosine of their angle (or the hyperbolic cosine of their inverse distance).

Setting , one obtains the analogous tetracyclic coordinates, which lead to circles instead of spheres.

Completely analogous constructions can be performed for spaces of higher dimensions, which give polyspherical coordinates. In the 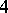-dimensional case they are called hexaspherical coordinates. Polyspherical coordinates are used in conformal geometry in examining manifolds of figures.

References

[1]	F. Klein, "Vorlesungen über höhere Geometrie" , Springer (1926)
[2]	G.V. Bushmanova, A.P. Norden, "Elements of conformal geometry" , Kazan' (1972) (In Russian)

References

[a1]	M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French)
[a2]	J.L. Coolidge, "A treatise on the circle and the sphere" , Chelsea, reprint (1971)