Weierstrass coordinates
A type of coordinates in an elliptic space. Let 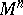 be an elliptic space obtained by the identification of diametrically-opposite points of the unit sphere
be an elliptic space obtained by the identification of diametrically-opposite points of the unit sphere 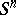 in
in 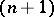 -dimensional Euclidean space. The Weierstrass coordinates
-dimensional Euclidean space. The Weierstrass coordinates 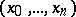 of a point in
of a point in 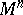 are the orthogonal Cartesian coordinates of the point of
are the orthogonal Cartesian coordinates of the point of 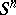 that corresponds to it. Since the isometric mapping of
that corresponds to it. Since the isometric mapping of 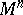 into
into 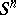 is not single-valued, Weierstrass coordinates are defined up to sign. A hyperplane in
is not single-valued, Weierstrass coordinates are defined up to sign. A hyperplane in 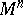 is given by a homogeneous linear equation
is given by a homogeneous linear equation
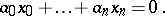 |
Named after K. Weierstrass, who used these coordinates in his courses on Lobachevskii geometry in 1872.
Comments
These coordinates for elliptic space can be normalized so that
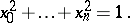 |
The analogous Weierstrass coordinates for hyperbolic space satisfy
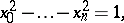 |
with the same equation  for a hyperplane.
for a hyperplane.
References
| [a1] | H. Liebmann, "Nichteuklidische Geometrie" , Göschen (1912) pp. 114–119 |
| [a2] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 121, 281 |
Weierstrass coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_coordinates&oldid=15072