Vague topology

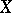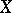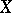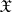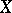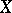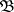Let be a locally compact Hausdorff space. Assume that is second countable (i.e. there is a countable base). Then is a Polish space (there exists a complete separable metrization). Let be the Borel field of (cf. Borel field of sets), generated by the (set of open subsets of the) topology of . Let be the ring of all relatively compact elements of 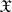, the ring of bounded Borel sets. Let 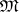be the collection of all Borel measures on 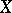(cf. Borel measure). Let 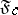be the space of real-valued functions of compact support on 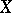. A sequence of elements 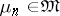converges to 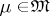if for all ,

(*)

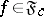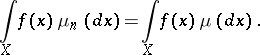The topology thus obtained on 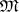is called the vague topology. If (*) is required to hold for all bounded continuous functions, one obtains the weak topology on 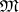. Thus, the vague topology is weaker than the weak topology. The difference is illustrated by the observation that a subset 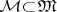is relatively compact in the vague topology if and only if 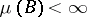for all 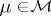and is relatively compact in the weak topology if and only if 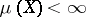for all 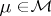and .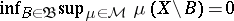

Let 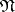be the set of all integer-valued elements of 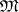, i.e. those 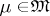for which 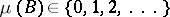for all 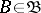. Then 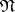is vaguely closed in 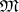. Both 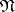and 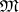are Polish in the vague topology.

If a sequence of real random variables 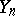on a probability space 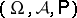converges in probability (cf. Convergence in probability) to a random variable 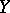, then their associated measures converge vaguely. If 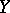is 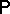-almost surely constant, the converse also holds.

References

[a1]	H. Bauer, "Probability theory and elements of measure theory" , Holt, Rinehart & Winston (1972) pp. §7.7 (Translated from German)
[a2]	O. Kallenberg, "Random measures" , Akademie Verlag & Acad. Press (1986) pp. Chapt. 15
[a3]	J. Grandell, "Doubly stochastic Poisson processes" , Springer (1976) pp. Appendix
[a4]	N. Bourbaki, "Intégration" , Eléments de mathématiques , Hermann (1965) pp. Chapt. 1–4, §3.9