Zorich theorem
From Encyclopedia of Mathematics
In 1967, V.A. Zorich proved the following result for quasi-regular mappings in space (see also Quasi-regular mapping): A locally homeomorphic quasi-regular mapping 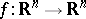 ,
, 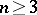 , is, in fact, a homeomorphism of
, is, in fact, a homeomorphism of 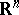 .
.
This result had been conjectured by M.A. Lavrent'ev in 1938. Note that the exponential function shows that there is no such result for  . In 1971, O. Martio, S. Rickman and J. Väisälä proved a stronger quantitative result: For
. In 1971, O. Martio, S. Rickman and J. Väisälä proved a stronger quantitative result: For 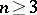 and
and 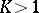 there exists a number
there exists a number 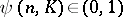 , the radius of injectivity, such that every locally injective
, the radius of injectivity, such that every locally injective 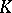 -quasi-regular mapping
-quasi-regular mapping 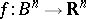 , where
, where 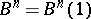 and
and 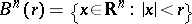 , for
, for 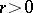 , is injective in
, is injective in 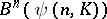 .
.
References
| [a1] | S. Rickman, "Quasiregular mappings" , Ergeb. Math. Grenzgeb. , 26 , Springer (1993) |
| [a2] | V.A. Zorich, "The global homeomorphism theorem for space quasiconformal mappings, its development and related open problems" M. Vuorinen (ed.) , Quasiconformal Space Mappings , Lecture Notes in Mathematics , 1508 (1992) pp. 132–148 |
| [a3] | O. Martio, U. Sebro, "Universal radius of injectivity for locally quasiconformal mappings" Israel J. Math. , 29 (1978) pp. 17–23 |
How to Cite This Entry:
Zorich theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zorich_theorem&oldid=15060
Zorich theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zorich_theorem&oldid=15060
This article was adapted from an original article by M. Vuorinen (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article