Schröder functional equation

The equation

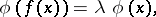(a1)

where 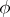is the unknown function and 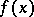is a known real-valued function of a real variable . I.e. one asks for the eigenvalues and eigenfunctions of the composition operator (substitution operator) 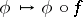. Sometimes 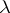is allowed to be a function itself.

One also considers the non-autonomous Schröder functional equation

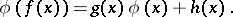The Schröder and Abel functional equations (see also Functional equation) have much to do with the translation functional equation

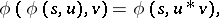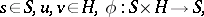where 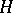is a semi-group, which asks for something like a right action of 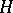on , [a1], [a4].

The equation was formulated by E. Schröder, [a5], and there is an extensive body of literature.

References

[a1]	J. Aczél, "A short course on functional equations" , Reidel (1987)
[a2]	M. Kuczma, "On the Schröder operator" , PWN (1963)
[a3]	M. Kuczma, "Functional equations in a single variable" , PWN (1968)
[a4]	G. Targonski, "Topics in iteration theory" , Vandenhoeck and Ruprecht (1981) pp. 82ff.
[a5]	E. Schröder, "Uber iterierte Funktionen III" Math. Ann. , 3 (1970) pp. 296–322
[a6]	J. Walorski, "Convex solutions of the Schröder equation in Banach spaces" Proc. Amer. Math. Soc. , 125 (1997) pp. 153–158