Stochastic integral

An integral "∫ H dX" with respect to a semi-martingale on some stochastic basis , defined for every locally bounded predictable process 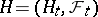. One of the possible constructions of a stochastic integral is as follows. At first a stochastic integral is defined for simple predictable processes , of the form

where is -measurable. In this case, by the stochastic integral 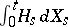(or , or ) one understands the variable

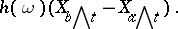The mapping 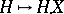, where

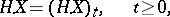permits an extension (also denoted by ) onto the set of all bounded predictable functions, which possesses the following properties:

a) the process 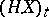, , 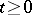is continuous from the right and has limits from the left;

b) is linear, i.e.

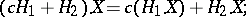c) If 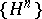is a sequence of uniformly-bounded predictable functions, 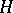is a predictable function and

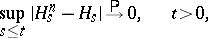then

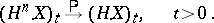The extension 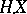is therefore unique in the sense that if 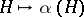is another mapping with the properties a)–c), then 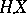and 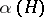are stochastically indistinguishable (cf. Stochastic indistinguishability).

The definition

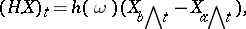given for functions holds for any process 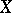, not only for semi-martingales. The extension 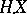with properties a)–c) onto the class of bounded predictable processes is only possible for the case where 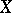is a semi-martingale. In this sense, the class of semi-martingales is the maximal class for which a stochastic integral with the natural properties a)–c) is defined.

If 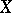is a semi-martingale and 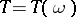is a Markov time (stopping time), then the "stopped" process 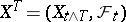is also a semi-martingale and for every predictable bounded process ,

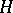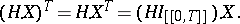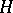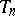This property enables one to extend the definition of a stochastic integral to the case of locally-bounded predictable functions . If is a localizing (for 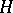) sequence of Markov times, then the 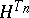are bounded. Hence, the 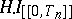are bounded and

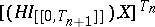is stochastically indistinguishable from 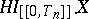. A process , again called a stochastic integral, therefore exists, such that

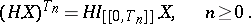The constructed stochastic integral 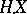possesses the following properties: is a semi-martingale; the mapping 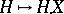is linear; if is a process of locally bounded variation, then so is the integral 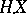, and 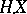then coincides with the Stieltjes integral of 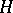with respect to ; ; .

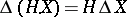Depending on extra assumptions concerning 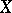, the stochastic integral 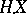can also be defined for broader classes of functions 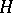. For example, if 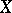is a locally square-integrable martingale, then a stochastic integral 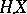(with the properties a)–c)) can be defined for any predictable process 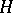that possesses the property that the process

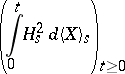is locally integrable (here 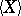is the quadratic variation of 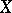, i.e. the predictable increasing process such that is a local martingale).

References

[1]	J. Jacod, "Calcul stochastique et problèmes de martingales" , Lect. notes in math. , 714 , Springer (1979)
[2]	C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A-C , North-Holland (1978–1988) (Translated from French)
[3]	R.Sh. Liptser, A.N. [A.N. Shiryaev] Shiryayev, "Theory of martingales" , Kluwer (1989) (Translated from Russian)

Comments

The result alluded to above, that semi-martingales constitute the widest viable class of stochastic integrators, is the Bichteler–Dellacherie theorem [a1]–[a3], and can be formulated as follows [a4], Thm. III.22. Call a process elementary predictable if it has a representation

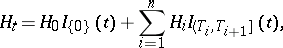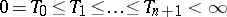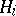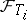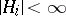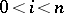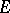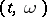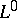where are stopping times and is -measurable with a.s., . Let be the set of elementary predictable processes, topologized by uniform convergence in . Let be the set of finite-valued random variables, topologized by convergence in probability. Fix a stochastic process 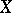and for each stopping time 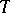define a mapping 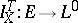by

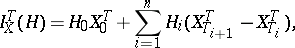where 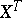denotes the process 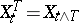. Say that "X has the property (C)" if 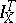is continuous for all stopping times.

The Bichteler–Dellacherie theorem: 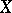has property (C) if and only if 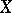is a semi-martingale.

Since the topology on 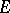is very strong and that on 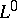very weak, property (C) is a minimal requirement if the definition of 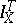is to be extended beyond .

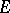It is possible to use property (C) as the definition of a semi-martingale, and to develop the theory of stochastic integration from this point of view [a4]. There are many excellent textbook expositions of stochastic integration from the conventional point of view; see, e.g., [a5]–[a8].

References

[a1]	K. Bichteler, "Stochastic integrators" Bull. Amer. Math. Soc. , 1 (1979) pp. 761–765
[a2]	K. Bichteler, "Stochastic integrators and the theory of semimartingales" Ann. Probab. , 9 (1981) pp. 49–89
[a3]	C. Dellacherie, "Un survol de la théorie de l'intégrale stochastique" Stoch. Proc. & Appl. , 10 (1980) pp. 115–144
[a4]	P. Protter, "Stochastic integration and differential equations" , Springer (1990)
[a5]	K.L. Chung, R.J. Williams, "Introduction to stochastic integration" , Birkhäuser (1990)
[a6]	R.J. Elliott, "Stochastic calculus and applications" , Springer (1982)
[a7]	I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1988)
[a8]	L.C.G. Rogers, D. Williams, "Diffusions, Markov processes and martingales" , II. Ito calculus , Wiley (1987)
[a9]	H.P. McKean jr., "Stochastic integrals" , Acad. Press (1969)
[a10]	M. Metivier, J. Pellaumail, "Stochastic integration" , Acad. Press (1980)
[a11]	E.J. McShane, "Stochastic calculus and stochastic models" , Acad. Press (1974)
[a12]	M.M. Rao, "Stochastic processes and integration" , Sijthoff & Noordhoff (1979)
[a13]	D.W. Stroock, S.R.S. Varadhan, "Multidimensional diffusion processes" , Springer (1979)
[a14]	P.E. Kopp, "Martingales and stochastic integrals" , Cambridge Univ. Press (1984)
[a15]	M. Fukushima, "Dirichlet forms and Markov processes" , North-Holland (1980)
[a16]	S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Nonstandard methods in stochastic analysis and mathematical physics" , Acad. Press (1986)