Poly-analytic function

of order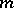

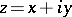A complex function of the real variables and , or, which is equivalent, of the complex variables and 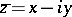, in a plane domain 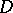which can be represented as

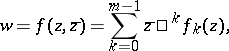(1)

where 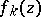, , 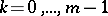are complex-analytic functions in 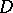. In other words, a poly-analytic function 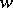of order 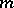can be defined as a function which in 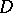has continuous partial derivatives with respect to and 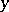, or with respect to and , up to order 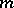inclusive and which everywhere in 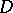satisfies the generalized Cauchy–Riemann condition:

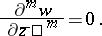For 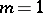one obtains analytic functions (cf. Analytic function).

For a function 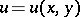to be the real (or imaginary) part of some poly-analytic function in a domain 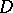, it is necessary and sufficient that be a poly-harmonic function in 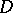. One can transfer to poly-analytic functions certain classical properties of analytic functions, with appropriate changes (see [1]).

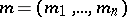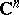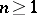A poly-analytic function of multi-order in the complex variables and in a domain of the complex space , , is a function of the form

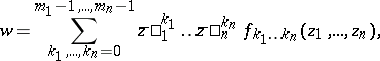where 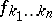are analytic functions of the variables in .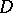

References

[1]	M.B. Balk, M.F. Zuev, "On polyanalytic functions" Russian Math. Surveys , 25 : 5 (1970) pp. 201–223 Uspekhi Mat. Nauk , 25 : 5 (1970) pp. 203–226