Problems on the distribution of deformation and stress in a system of solid bodies having parts of their boundaries in common (surfaces of contact). In a general formulation, results on contact problems are restricted to existence theorems and certain approximate methods of solution. More complete results relate to the case when one of the contacting bodies is an elastic half-plane (or half-space), while the other is an absolutely-rigid body impressed into the half-plane (or half-space) by given forces (the problem of stamps). Outside the base of the stamp coming into contact with the elastic body, the boundary conditions on the latter can be given arbitrarily from a number of admissible ones, while on the part underneath the stamp, the boundary conditions are stated in accordance with the nature of contact. Thus, if the elastic body is firmly coupled to the rigid body that is to be pressed, then the displacement under the stamp can be considered prescribed; if on the other hand, the elastic body is allowed to slide along the contact surface of the rigid stamp, then under the stamp the normal component of the displacement is known as well as a certain linear relation between the normal and tangential stresses, depending on the coefficient of friction (Coulomb's law). Other boundary conditions can also be realized. All cases of an elastic half-plane (half-space) reduce to a mixed problem with various boundary conditions on various parts of the boundary. The subject matter of papers devoted to stamp problems consists of the development of methods for solving these problems, including the case when both bodies in contact are elastic. These methods are close to one another and in the planar case, in the final event, reduce to a method of conjugation of piecewise-holomorphic functions (the method of the Riemann–Hilbert problem), by means of which the contact problems are solved in quadratures. The problem of contact of two elastic bodies in the three-dimensional case was first posed and solved by H. Hertz, who considered the area of contact to be very small and the equations of the undeformed surfaces near the place of contact as equations of second-order surfaces. Here it proves possible to use one of the electrostatic analogues, and the function expressing the impression in the region of contact is found in the form of the electrostatic potential of a certain ellipsoid. In the planar case, Hertz' problem reduces to the first-order Fredholm equation
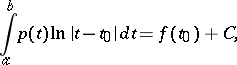 |
where 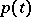 is the required stress of one body on another at the point
is the required stress of one body on another at the point 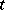 of the region of contact
of the region of contact 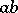 and
and 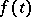 is a given function; this problem reduces to a singular integral equation that is solvable in closed form.
is a given function; this problem reduces to a singular integral equation that is solvable in closed form.
In the general formulation the contact problem is stated in the following way.
Problem I) Suppose that in an infinite isotropic elastic body with Lamé constants 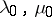 there are
there are 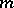 elastic isotropic isolated cut-ins with constants
elastic isotropic isolated cut-ins with constants  ,
, 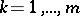 , bounded by smooth surfaces
, bounded by smooth surfaces 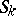 of arbitrary configuration. Considering the cut-ins to be rigidly fastened to the base medium along the contact surfaces
of arbitrary configuration. Considering the cut-ins to be rigidly fastened to the base medium along the contact surfaces 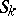 , it is required to determine the stress condition of the body under the influence of given volumetric pressures.
, it is required to determine the stress condition of the body under the influence of given volumetric pressures.
Problem II) In a finite isotropic elastic body with arbitrary smooth boundary 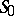 and Lamé constants
and Lamé constants 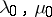 there are
there are 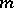 elastic isotropic isolated cut-ins bounded by surfaces
elastic isotropic isolated cut-ins bounded by surfaces 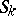 ,
, 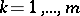 , rigidly fastened to the supporting medium along
, rigidly fastened to the supporting medium along 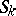 . It is required to find the elastic state of the body as a result of the action of given volumetric pressures and given boundary conditions on
. It is required to find the elastic state of the body as a result of the action of given volumetric pressures and given boundary conditions on 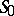 .
.
These same problems can be posed for anisotropic bodies as well as under other assumptions regarding the nature of the contacts along 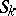 ,
,  . Existence theorems have been proved for these problems, in the isotropic case by the method of singular potentials and singular integral equations, and for anisotropic bodies by methods of functional analysis.
. Existence theorems have been proved for these problems, in the isotropic case by the method of singular potentials and singular integral equations, and for anisotropic bodies by methods of functional analysis.
In the isotropic case methods of approximate solution in quadratures have also been found. Let 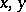 be points from the three-dimensional space
be points from the three-dimensional space 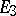 , let
, let 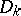 be the region bounded by the surface
be the region bounded by the surface 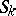 ,
,  ,
, 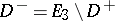 , let
, let 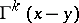 be the
be the 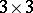 matrix of fundamental solutions for
matrix of fundamental solutions for 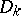 ,
, 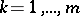 , let
, let 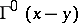 be the same matrix for
be the same matrix for 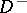 , let
, let 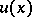 be the displacement vector at
be the displacement vector at  , let
, let 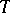 be the stress operator and
be the stress operator and 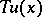 the stress vector corresponding to the displacement
the stress vector corresponding to the displacement  at
at  , let
, let 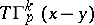 ,
, 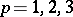 , be the stress vector corresponding to the displacement
, be the stress vector corresponding to the displacement 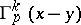 in
in 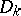 for
for 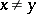 , let
, let 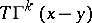 be the
be the 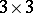 matrix with columns
matrix with columns 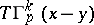 ,
, 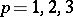 , and let
, and let 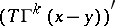 be the adjoint matrix. The
be the adjoint matrix. The 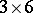 matrices
matrices 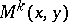 and
and 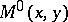 are defined as follows
are defined as follows 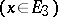 ,
,
Problem I, without loss of generality, is one of determining the displacement from the conditions
Let the values of the limits on both sides of the contact boundaries for 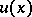 and
and 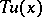 be denoted by
be denoted by 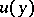 ,
, 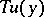 ,
, 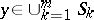 ; then for the regular solution:
; then for the regular solution:
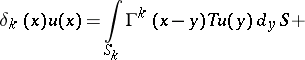 | (1a) |
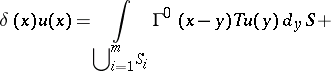 | (1b) |
where
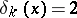 for
for 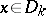 , while
, while 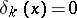 for
for 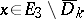 ;
; 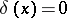 for
for 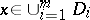 and
and 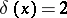 for
for 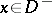 .
.
Formulas
can be written in the form:
where 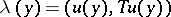 is a six-dimensional vector. The first of these equations holds for all
is a six-dimensional vector. The first of these equations holds for all  belonging to
belonging to 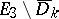 , while the second holds for all
, while the second holds for all  belonging to
belonging to 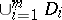 . The corresponding arbitrarily given values of the variable
. The corresponding arbitrarily given values of the variable  lead to the infinite set of equations
lead to the infinite set of equations
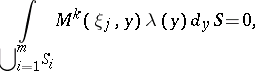 | (2a) |
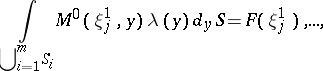 | (2b) |
Let 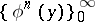 be the set of six-dimensional vectors
be the set of six-dimensional vectors
correspondingly indexed, for example, by the diagonal rule. This set is linearly independent and complete in 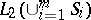 . On the left-hand sides of
. On the left-hand sides of
are the scalar products 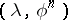 for any value of the index
for any value of the index  , which serve as the components of the given vectors and therefore these products are also given. Because of the completeness of
, which serve as the components of the given vectors and therefore these products are also given. Because of the completeness of 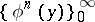 in
in 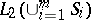 , the unknown vector
, the unknown vector 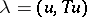 can be approximated by a linear combination
can be approximated by a linear combination 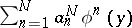 if the constants
if the constants 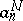 are found from the condition that the norm
are found from the condition that the norm
is minimal.
This leads to the system of linear algebraic equations
which is solvable. The 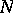 -th approximation
-th approximation 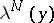 for the vector
for the vector 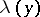 is expressed by the formula
is expressed by the formula 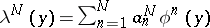 .
.
Substituting the first three components of 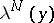 , as a vector, in place of
, as a vector, in place of 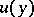 , and the second three components in place of
, and the second three components in place of 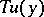 in the integrands in , one obtains an approximate solution of Problem I in quadratures. The exact solution is the uniform limit as
in the integrands in , one obtains an approximate solution of Problem I in quadratures. The exact solution is the uniform limit as 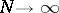 at any interior point of the region.
at any interior point of the region.
The formulas for the solution of Problem II are the same apart from one modification: Instead of the matrix 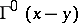 the Green tensor corresponding to the boundary conditions defined on
the Green tensor corresponding to the boundary conditions defined on 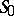 is used for the total region bounded by the surface
is used for the total region bounded by the surface 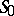 .
.
References
| [1] | N.I. Muskhelishvili, "Some basic problems of the mathematical theory of elasticity" , Noordhoff (1975) (Translated from Russian) |
| [2] | L.A. Galin, "Contact problems in the theory of elasticity" , Moscow (1953) (In Russian) |
| [3] | I.Ya. Shtaerman, "Contact problems of the theory of elasticity" , Moscow-Leningrad (1949) (In Russian) |
| [4] | V.D. Kupradze, T.V. Burchuladze, T.G. Gegelia, M.O. Basheleishvili, "Three-dimensional problems of the mathematical theory of elasticity and thermoelasticity" , North-Holland (1979) (Translated from Russian) |
| [5] | G. Fichera, "Existence theorems in elasticity" , Handbuch der Physik , VIa/2 , Springer (1973) pp. 347–389 |
References
| [a1] | G.M.L. Gladwell, "Contact problems in the classical theory of elasticity" , Sijthoff & Noordhoff (1980) |
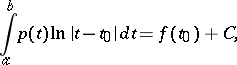
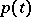 is the required stress of one body on another at the point
is the required stress of one body on another at the point 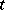 of the region of contact
of the region of contact 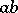 and
and 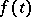 is a given function; this problem reduces to a singular integral equation that is solvable in closed form.
is a given function; this problem reduces to a singular integral equation that is solvable in closed form.
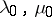 there are
there are 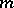 elastic isotropic isolated cut-ins with constants
elastic isotropic isolated cut-ins with constants  ,
, 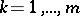 , bounded by smooth surfaces
, bounded by smooth surfaces 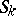 of arbitrary configuration. Considering the cut-ins to be rigidly fastened to the base medium along the contact surfaces
of arbitrary configuration. Considering the cut-ins to be rigidly fastened to the base medium along the contact surfaces 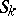 , it is required to determine the stress condition of the body under the influence of given volumetric pressures.
, it is required to determine the stress condition of the body under the influence of given volumetric pressures.
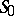 and Lamé constants
and Lamé constants 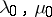 there are
there are 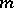 elastic isotropic isolated cut-ins bounded by surfaces
elastic isotropic isolated cut-ins bounded by surfaces 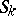 ,
, 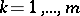 , rigidly fastened to the supporting medium along
, rigidly fastened to the supporting medium along 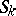 . It is required to find the elastic state of the body as a result of the action of given volumetric pressures and given boundary conditions on
. It is required to find the elastic state of the body as a result of the action of given volumetric pressures and given boundary conditions on 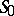 .
.
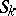 ,
,  . Existence theorems have been proved for these problems, in the isotropic case by the method of singular potentials and singular integral equations, and for anisotropic bodies by methods of functional analysis.
. Existence theorems have been proved for these problems, in the isotropic case by the method of singular potentials and singular integral equations, and for anisotropic bodies by methods of functional analysis.
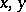 be points from the three-dimensional space
be points from the three-dimensional space 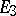 , let
, let 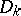 be the region bounded by the surface
be the region bounded by the surface 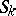 ,
,  ,
, 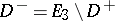 , let
, let 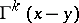 be the
be the 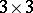 matrix of fundamental solutions for
matrix of fundamental solutions for 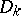 ,
, 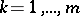 , let
, let 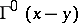 be the same matrix for
be the same matrix for 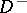 , let
, let 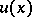 be the displacement vector at
be the displacement vector at  , let
, let 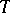 be the stress operator and
be the stress operator and 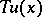 the stress vector corresponding to the displacement
the stress vector corresponding to the displacement  at
at  , let
, let 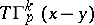 ,
, 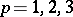 , be the stress vector corresponding to the displacement
, be the stress vector corresponding to the displacement 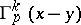 in
in 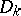 for
for 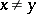 , let
, let 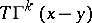 be the
be the 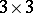 matrix with columns
matrix with columns 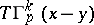 ,
, 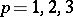 , and let
, and let 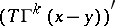 be the adjoint matrix. The
be the adjoint matrix. The 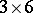 matrices
matrices 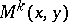 and
and 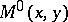 are defined as follows
are defined as follows 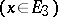 ,
,
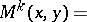
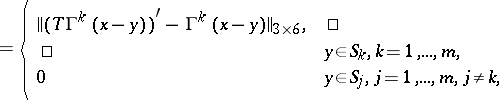
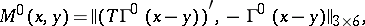
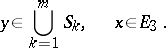
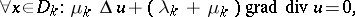
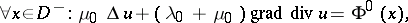
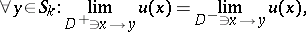
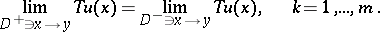
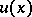 and
and 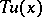 be denoted by
be denoted by 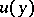 ,
, 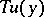 ,
, 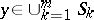 ; then for the regular solution:
; then for the regular solution:
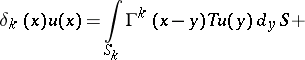
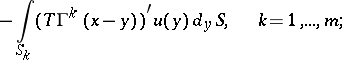
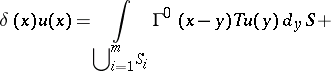
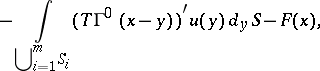
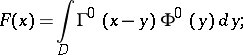
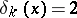 for
for 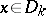 , while
, while 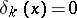 for
for 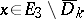 ;
; 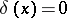 for
for 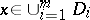 and
and 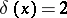 for
for 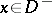 .
.
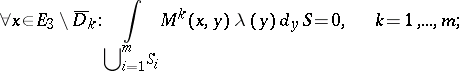
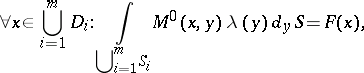
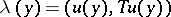 is a six-dimensional vector. The first of these equations holds for all
is a six-dimensional vector. The first of these equations holds for all  belonging to
belonging to 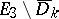 , while the second holds for all
, while the second holds for all  belonging to
belonging to 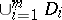 . The corresponding arbitrarily given values of the variable
. The corresponding arbitrarily given values of the variable  lead to the infinite set of equations
lead to the infinite set of equations
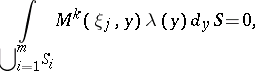
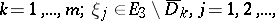
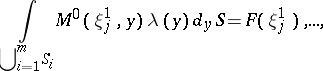

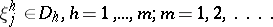
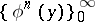 be the set of six-dimensional vectors
be the set of six-dimensional vectors
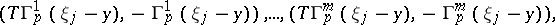
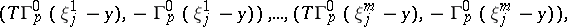
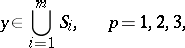
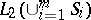 . On the left-hand sides of
. On the left-hand sides of
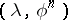 for any value of the index
for any value of the index  , which serve as the components of the given vectors and therefore these products are also given. Because of the completeness of
, which serve as the components of the given vectors and therefore these products are also given. Because of the completeness of 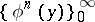 in
in 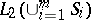 , the unknown vector
, the unknown vector 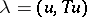 can be approximated by a linear combination
can be approximated by a linear combination 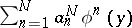 if the constants
if the constants 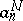 are found from the condition that the norm
are found from the condition that the norm
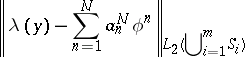
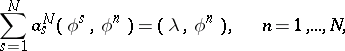
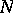 -th approximation
-th approximation 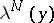 for the vector
for the vector 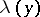 is expressed by the formula
is expressed by the formula 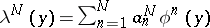 .
.
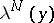 , as a vector, in place of
, as a vector, in place of 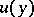 , and the second three components in place of
, and the second three components in place of 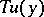 in the integrands in , one obtains an approximate solution of Problem I in quadratures. The exact solution is the uniform limit as
in the integrands in , one obtains an approximate solution of Problem I in quadratures. The exact solution is the uniform limit as 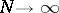 at any interior point of the region.
at any interior point of the region.
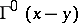 the Green tensor corresponding to the boundary conditions defined on
the Green tensor corresponding to the boundary conditions defined on 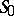 is used for the total region bounded by the surface
is used for the total region bounded by the surface 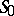 .
.