Functional separability
The property of two sets 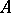 and
and  in a topological space
in a topological space 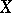 requiring the existence of a continuous real-valued function
requiring the existence of a continuous real-valued function 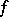 on
on 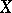 such that the closures of the sets
such that the closures of the sets 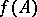 and
and 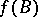 (relative to the usual topology on the real line
(relative to the usual topology on the real line 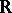 ) do not intersect. For example, a space is completely regular if every closed set is separable from each one-point set that does not intersect it. A space is normal if every two closed non-intersecting subsets of it are functionally separable. If every two (distinct) one-point sets in a space are functionally separable, then the space is called functionally Hausdorff. The content of these definitions is unchanged if, instead of continuous real-valued functions, one takes continuous mappings into the plane, into an interval or into the Hilbert cube.
) do not intersect. For example, a space is completely regular if every closed set is separable from each one-point set that does not intersect it. A space is normal if every two closed non-intersecting subsets of it are functionally separable. If every two (distinct) one-point sets in a space are functionally separable, then the space is called functionally Hausdorff. The content of these definitions is unchanged if, instead of continuous real-valued functions, one takes continuous mappings into the plane, into an interval or into the Hilbert cube.
References
| [1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
| [2] | J.L. Kelley, "General topology" , Springer (1975) |
Functional separability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functional_separability&oldid=14738