Presentation

of a group

A specification of a group by generators and relations among them.

Comments

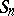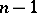Every group can be presented by means of generators and relations. A presentation is finitely generated, respectively finitely related, if the number of generators, respectively relations, is finite. A finite presentation is one with both a finite number of relations and a finite number of generators. A presentation of the symmetric group of permutations on letters is as follows: there are generators 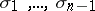, and the relations are 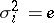, if 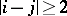, 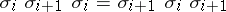. If the relations 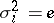are removed, one obtains a presentation of the braid group (cf. Braid theory).

If 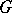is presented by generators 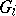, , 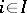and relations 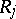, , 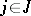one writes 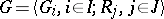. In that case 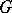is the quotient group of the free group on the generators 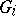by the normal subgroup generated by the relations 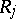. For details cf. [a1], Sect. 1.2. Given a presentation of a group, there are systematic ways for obtaining presentations of subgroups and quotient groups.

References

[a1]	W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations of groups in terms of generators and relations" , Wiley (Interscience) (1966)
[a2]	H.S.M. Coxeter, W.O.J. Moser, "Generators and relations for discrete groups" , Springer (1965)