Lie differentiation
A natural operation on a differentiable manifold 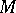 that associates with a differentiable vector field
that associates with a differentiable vector field 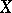 and a differentiable geometric object
and a differentiable geometric object 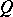 on
on 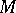 (cf. Geometric objects, theory of) a new geometric object
(cf. Geometric objects, theory of) a new geometric object 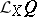 , which describes the rate of change of
, which describes the rate of change of 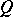 with respect to the one-parameter (local) transformation group
with respect to the one-parameter (local) transformation group 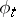 of
of 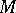 generated by
generated by  . The geometric object
. The geometric object 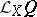 is called the Lie derivative of the geometric object
is called the Lie derivative of the geometric object 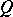 with respect to
with respect to  (cf. also Lie derivative). Here it is assumed that transformations of
(cf. also Lie derivative). Here it is assumed that transformations of 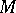 induce transformations in the space of objects
induce transformations in the space of objects 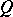 in a natural way.
in a natural way.
In the special case when 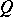 is a vector-valued function on
is a vector-valued function on 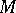 , its Lie derivative
, its Lie derivative 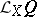 coincides with the derivative
coincides with the derivative  of the function
of the function 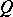 in the direction of the vector field
in the direction of the vector field 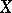 and is given by the formula
and is given by the formula
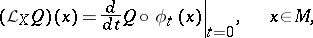 |
where 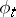 is the one-parameter local transformation group on
is the one-parameter local transformation group on 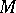 generated by
generated by 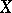 , or, in the local coordinates
, or, in the local coordinates 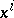 , by the formula
, by the formula
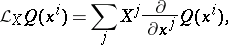 |
where
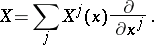 |
In the general case the definition of Lie differentiation consists in the following. Let 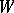 be a
be a 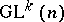 -space, that is, a manifold with a fixed action of the general differential group
-space, that is, a manifold with a fixed action of the general differential group 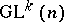 of order
of order 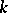 (the group of
(the group of 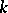 -jets at the origin of diffeomorphisms
-jets at the origin of diffeomorphisms 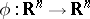 ,
, 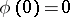 ). Let
). Let 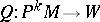 be a geometric object of order
be a geometric object of order 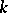 and type
and type 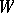 on an
on an  -dimensional manifold
-dimensional manifold 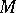 , regarded as a
, regarded as a 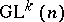 -equivariant mapping of the principal
-equivariant mapping of the principal 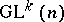 -bundle of coframes
-bundle of coframes 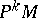 of order
of order 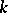 on
on 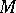 into
into 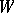 . The one-parameter local transformation group
. The one-parameter local transformation group 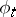 on
on 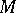 generated by a vector field
generated by a vector field 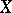 on
on 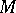 induces a one-parameter local transformation group
induces a one-parameter local transformation group 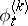 on the manifold of coframes
on the manifold of coframes 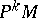 . Its velocity field
. Its velocity field
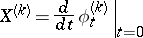 |
is called the complete lift of 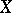 to
to 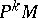 . The Lie derivative of a geometric object
. The Lie derivative of a geometric object 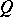 of type
of type 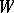 with respect to a vector field
with respect to a vector field 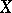 on
on 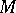 is defined as the geometric object
is defined as the geometric object 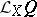 of type
of type 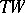 (where
(where 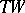 is the tangent bundle of
is the tangent bundle of 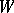 , regarded in a natural way as a
, regarded in a natural way as a 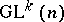 -space), given by the formula
-space), given by the formula
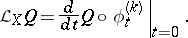 |
The value of the Lie derivative 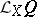 at a point
at a point 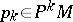 depends only on the
depends only on the 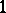 -jet of
-jet of 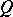 at
at  , and does so linearly, and on the value of
, and does so linearly, and on the value of 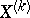 at this point (or, equivalently, on the
at this point (or, equivalently, on the 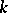 -jet of
-jet of 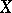 at the corresponding point
at the corresponding point  ).
).
If the geometric object 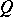 is linear, that is, the corresponding
is linear, that is, the corresponding  -space
-space 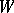 is a vector space with linear action of
is a vector space with linear action of 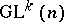 , then the tangent manifold
, then the tangent manifold 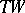 can in a natural way be identified with the direct product
can in a natural way be identified with the direct product 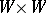 , and so the Lie derivative
, and so the Lie derivative
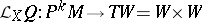 |
can be regarded as a pair of geometric objects of type 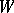 . The first of these is
. The first of these is 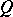 itself, and the second, which is usually identified with the Lie derivative of
itself, and the second, which is usually identified with the Lie derivative of 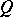 , is equal to the derivative
, is equal to the derivative 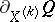 of
of 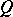 in the direction of the vector field
in the direction of the vector field 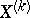 :
:
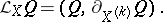 |
Thus, the Lie derivative of a linear geometric object can be regarded as a geometric object of the same type as 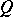 .
.
Local coordinates 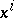 in the manifold
in the manifold 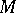 determine local coordinates
determine local coordinates  in the manifold
in the manifold 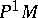 of coframes of order 1: for
of coframes of order 1: for 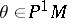 one has
one has
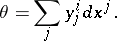 |
In these coordinates the Lie derivative of any geometric object 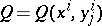 of order 1 (for example, a tensor field) in the direction of the vector field
of order 1 (for example, a tensor field) in the direction of the vector field
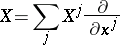 |
is given by the formula
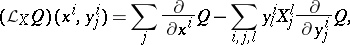 |
where
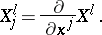 |
A similar formula holds for the Lie derivative of a geometric object of arbitrary order.
The Lie derivative 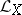 in the space of differential forms on a manifold
in the space of differential forms on a manifold 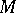 can be expressed in terms of the operator of exterior differentiation
can be expressed in terms of the operator of exterior differentiation 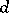 and the operator of interior multiplication
and the operator of interior multiplication  (defined as the contraction of a vector field with a differential form) by means of the following homotopy formula:
(defined as the contraction of a vector field with a differential form) by means of the following homotopy formula:
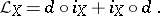 |
Conversely, the operator of exterior differentiation 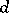 , acting on a
, acting on a  -form
-form 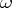 , can be expressed in terms of the Lie derivative by the formula
, can be expressed in terms of the Lie derivative by the formula
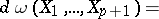 |
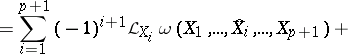 |
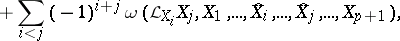 |
where  means that the corresponding symbol must be omitted, and the
means that the corresponding symbol must be omitted, and the 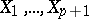 are vector fields.
are vector fields.
In contrast to covariant differentiation, which requires the introduction of a connection, the operation of Lie differentiation is determined by the structure of the differentiable manifold, and the Lie derivative of a geometric object  in the direction of a vector field
in the direction of a vector field 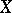 is a concomitant of the geometric objects
is a concomitant of the geometric objects 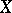 and
and 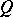 .
.
References
| [1] | W. Slebodziński, "Sur les équations canonique de Hamilton" Bull. Cl. Sci. Acad. Roy. Belgique , 17 (1931) pp. 864–870 |
| [2] | B.L. Laptev, "Lie differentiation" Progress in Math. , 6 (1970) pp. 229–269 Itogi. Nauk. Algebra Topol. Geom. 1965 (1967) pp. 429–465 |
| [3] | K. Yano, "The theory of Lie derivatives and its applications" , North-Holland (1957) |
| [4] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [5] | V.V. Vagner, "Theory of geometric objects and theory of finite and infinite continuous transformation groups" Dokl. Akad. Nauk SSSR , 46 (1945) pp. 347–349 (In Russian) |
| [6] | B.L. Laptev, "Lie derivative in a space of supporting elements" Trudy Sem. Vektor. Tenzor. Anal. , 10 (1956) pp. 227–248 (In Russian) |
| [7] | L.E. Evtushik, "The Lie derivative and differential field equations of a geometric object" Soviet Math. Dokl. , 1 (1960) pp. 687–690 Dokl. Akad. Nauk SSSR , 132 (1960) pp. 998–1001 |
| [8] | R.S. Palais, "A definition of the exterior derivative in terms of Lie derivatives" Proc. Amer. Math. Soc. , 5 (1954) pp. 902–908 |
Lie differentiation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_differentiation&oldid=14570