Enumeration operator
A mapping of the set of all sets of natural numbers into itself (i.e. a mapping of  into
into  , where
, where  is the set of natural numbers), defined as follows. Let
is the set of natural numbers), defined as follows. Let  be a recursively-enumerable set having Gödel number
be a recursively-enumerable set having Gödel number  , let
, let  be a finite set of natural numbers with canonical index
be a finite set of natural numbers with canonical index  (i.e.
(i.e.  , where
, where  and
and 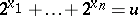 ) and let
) and let 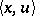 be the number of the ordered pair consisting of the numbers
be the number of the ordered pair consisting of the numbers  and
and  for a certain specified one-to-one recursive encoding of the pairs. Each recursively-enumerable set
for a certain specified one-to-one recursive encoding of the pairs. Each recursively-enumerable set 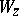 yields a procedure that transforms any given set of natural numbers
yields a procedure that transforms any given set of natural numbers  into the set
into the set 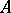 of natural numbers
of natural numbers  with the property that
with the property that 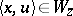 for some
for some  with
with 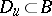 , i.e.
, i.e. 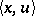 belongs to
belongs to 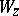 and if the finite set
and if the finite set 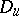 is contained in
is contained in 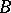 , then
, then  is related to
is related to 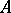 . In other words,
. In other words,
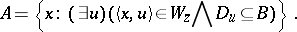 |
This procedure enables one to obtain effectively from any enumeration on 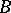 an enumeration on
an enumeration on 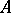 . It is called an enumeration operator and is denoted by
. It is called an enumeration operator and is denoted by 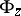 . If
. If 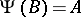 for some enumeration operator
for some enumeration operator 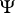 , one says that
, one says that  is reducible in enumerability to
is reducible in enumerability to  (
(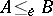 ).
).
If  and
and 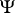 are enumeration operators, their composite
are enumeration operators, their composite 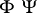 is also an enumeration operator. If
is also an enumeration operator. If 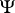 is an enumeration operator and
is an enumeration operator and 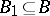 , then
, then 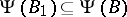 . If
. If  , then
, then  for some finite set
for some finite set 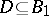 . Each enumeration operator
. Each enumeration operator 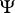 has a least fixed point, i.e. there exists a recursively-enumerable set
has a least fixed point, i.e. there exists a recursively-enumerable set  such that
such that 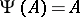 , and if
, and if  , then
, then 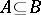 .
.
References
| [1] | H. Rogers jr., "Theory of recursive functions and effective computability" , McGraw-Hill (1967) |
Enumeration operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Enumeration_operator&oldid=14496