Torsion tensor

A tensor of type 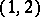that is skew-symmetric with respect to its indices, obtained by decomposing the torsion form of a connection in terms of a local cobasis on a manifold 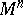. In particular, in terms of a holonomic cobasis 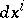, , 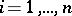the components 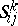of the torsion tensor are expressed in terms of the Christoffel symbols (cf. Christoffel symbol) 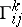of the connection as follows:

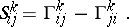Comments

In terms of covariant derivatives and vector fields 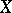, 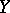the torsion tensor 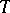can be described as follows:

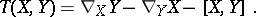References

[a1]	N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965)
[a2]	D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968)
[a3]	W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German)