Kripke models
Structures consisting of a certain set of ordinary models for classical logic, ordered by a certain relation, and serving for the interpretation of various non-classical logics (intuitionistic, modal, etc.). More precisely: A Kripke model for a language 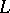 is given by
is given by
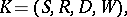 |
where 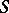 is a non-empty set (of "worlds" , "situations" );
is a non-empty set (of "worlds" , "situations" ); 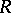 is a binary relation on
is a binary relation on 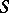 (for example, for the system
(for example, for the system 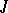 of intuitionistic logic,
of intuitionistic logic, 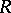 is a partial order; for the modal system (cf. Modal logic)
is a partial order; for the modal system (cf. Modal logic) 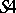 it is a pre-order; for the system
it is a pre-order; for the system 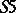 it is an equivalence relation);
it is an equivalence relation); 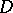 is a mapping which associates with each
is a mapping which associates with each 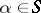 a non-empty domain
a non-empty domain 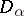 such that, if
such that, if 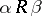 , then
, then 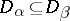 ;
; 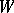 is a valuation which associates with each individual constant
is a valuation which associates with each individual constant  of the language
of the language 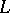 an element
an element 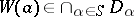 , and with each individual variable
, and with each individual variable  an element
an element 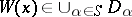 ; for each
; for each 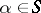 ,
, 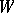 associates with each propositional variable
associates with each propositional variable 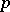 a truth value
a truth value 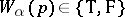 (for the system
(for the system 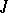 it is also stipulated that if
it is also stipulated that if 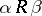 and
and  , then
, then 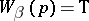 ); with each
); with each  -placed (
-placed (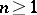 ) predicate symbol
) predicate symbol 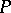 a certain subset
a certain subset 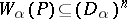 (for the system
(for the system 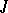 , if
, if  , then
, then 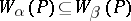 ); and with each
); and with each  -placed function symbol
-placed function symbol 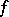 a function
a function 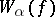 from
from 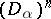 to
to 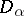 (for the system
(for the system 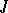 , if
, if 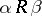 , then
, then 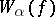 is the restriction of
is the restriction of 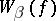 to
to 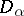 ).
).
For any 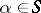 and any formula
and any formula 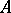 of
of 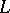 such that for each free variable
such that for each free variable  in
in 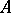 one has
one has 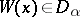 , the truth value
, the truth value 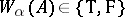 is defined inductively. For the system
is defined inductively. For the system  ,
, 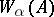 is defined as follows:
is defined as follows:
a) if 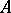 is an atomic formula,
is an atomic formula, 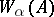 is already defined in the model;
is already defined in the model;
b) 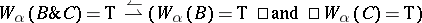 ;
;
c) 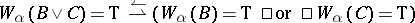 ;
;
d) 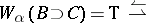 (for any
(for any 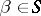 , if
, if 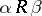 and
and 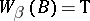 , then
, then 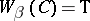 );
);
e) 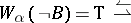 (for any
(for any 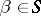 , if
, if 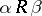 , then
, then 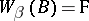 );
);
f) 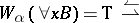 (for any
(for any 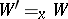 and
and 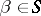 , if
, if 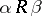 and
and 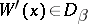 , then
, then 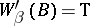 );
);
g) 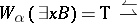 (there exists a
(there exists a 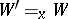 such that
such that 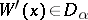 and
and 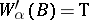 )
)
(here 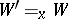 means that the valuation
means that the valuation 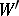 coincides with
coincides with 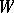 everywhere, except possibly on
everywhere, except possibly on  ). Instead of
). Instead of 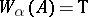 one sometimes writes
one sometimes writes 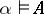 .
.
For modal logics, the definition of 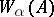 in cases d, e and g is different:
in cases d, e and g is different:
d') 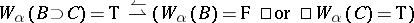 ;
;
e') 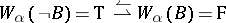 ;
;
g') 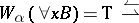 (for any
(for any 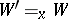 , if
, if 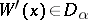 , then
, then 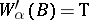 );
);
and, in addition, one requires
h) 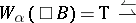 (for any
(for any 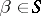 , if
, if 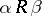 , then
, then 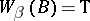 ).
).
A formula 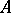 is said to be true in a Kripke model
is said to be true in a Kripke model 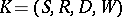 (written
(written 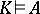 ) if
) if 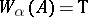 for any
for any 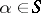 . For each of the systems
. For each of the systems 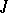 ,
, 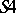 and
and 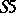 one has the completeness theorem: A formula is deducible in the system if and only if it is true in all Kripke models of the corresponding class. It is essential that the domains
one has the completeness theorem: A formula is deducible in the system if and only if it is true in all Kripke models of the corresponding class. It is essential that the domains 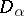 are in general different, since the formula
are in general different, since the formula
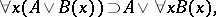 | (*) |
where  is not free in
is not free in 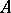 , is not deducible in
, is not deducible in  , but it is true in all Kripke models with constant domain. The system obtained from
, but it is true in all Kripke models with constant domain. The system obtained from 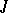 by adding the scheme (*) is complete relative to Kripke models with constant domain (see [3]). The propositional fragment of each of the systems
by adding the scheme (*) is complete relative to Kripke models with constant domain (see [3]). The propositional fragment of each of the systems 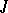 ,
, 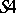 and
and 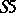 is finitely approximable, i.e. any formula which is not deducible in the system is refutable in some finite Kripke model of the corresponding class.
is finitely approximable, i.e. any formula which is not deducible in the system is refutable in some finite Kripke model of the corresponding class.
The concept of a "Kripke model" , due to S.A. Kripke, is related to that of forcing (see Forcing method).
References
| [1a] | S.A. Kripke, "A completeness theorem in modal logic" J. Symbolic Logic , 24 (1959) pp. 1–14 |
| [1b] | S.A. Kripke, "The undecidability of monadic modal quantification theory" Z. Math. Logik Grundl. Math. , 8 (1962) pp. 113–116 |
| [1c] | S.A. Kripke, "Semantical analysis of modal logic, I" Z. Math. Logik Grundl. Math. , 9 (1963) pp. 67–96 |
| [1d] | S.A. Kripke, "Semantical analysis of modal logic, II" J.W. Addison (ed.) L. Henkin (ed.) A. Tarski (ed.) , The theory of models , North-Holland (1965) pp. 206–220 |
| [2] | K. Schütte, "Vollständige Systeme modaler und intuitionistischer Logik" , Springer (1968) |
| [3] | S. Görnemann, "A logic stronger than intuitionism" J. Symbolic Logic , 36 (1971) pp. 249–261 |
| [4] | P.J. Cohen, "Set theory and the continuum hypothesis" , Benjamin (1966) |
Comments
Kripke models for intuitionistic logic are a special case of topos-theoretic models (cf. also Topos). Specifically, the function 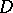 in the definition may be regarded as a pre-sheaf (i.e., a set-valued functor) on the partially ordered set
in the definition may be regarded as a pre-sheaf (i.e., a set-valued functor) on the partially ordered set 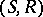 ; the function
; the function 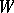 equips this pre-sheaf with a structure for the given language, internally in the topos of pre-sheaves on
equips this pre-sheaf with a structure for the given language, internally in the topos of pre-sheaves on 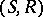 , and the inductive definition of validity, given above, is the external interpretation of internal validity in this topos. Kripke semantics remain sound (cf. also Sound rule) for models in any topos of pre-sheaves (that is, if the partial order
, and the inductive definition of validity, given above, is the external interpretation of internal validity in this topos. Kripke semantics remain sound (cf. also Sound rule) for models in any topos of pre-sheaves (that is, if the partial order 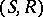 is replaced by an arbitrary small category
is replaced by an arbitrary small category 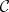 ) — one has only to replace the quantification over nodes
) — one has only to replace the quantification over nodes 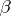 such that
such that 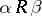 , which occurs in clauses d), e) and f), by a quantification over morphisms of
, which occurs in clauses d), e) and f), by a quantification over morphisms of 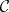 with domain
with domain 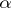 . However, if one considers models in a topos of sheaves (that is, if one introduces a Grothendieck topology on the category
. However, if one considers models in a topos of sheaves (that is, if one introduces a Grothendieck topology on the category 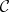 ), then clauses c) and g) have to be modified in order to take into account the covering families of the topology; for example, c) becomes
), then clauses c) and g) have to be modified in order to take into account the covering families of the topology; for example, c) becomes
c') 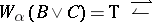 there exists a covering family of morphisms with domain
there exists a covering family of morphisms with domain 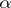 , such that for every
, such that for every 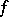 in the family either
in the family either 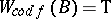 or
or 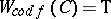 .
.
The resulting interpretation is commonly called Kripke–Joyal semantics (after A. Joyal).
For more detailed accounts, see [a1] or [a2].
References
| [a1] | R.I. Goldblatt, "Topoi: the categorial analysis of logic" , North-Holland (1979) |
| [a2] | J.L. Bell, "Toposes and local set theories" , Oxford Univ. Press (1988) |
| [a3] | M.A.E. Dummett, "Elements of intuitionism" , Oxford Univ. Press (1977) |
| [a4] | S. Kripke, "Semantical considerations on modal and intuitionistic logic" Acta Philos. Fennica , 16 (1963) pp. 83–94 |
| [a5] | S.A. Kripke, "Semantical analysis of intuitionistic logic, I" J.N. Crossley (ed.) M.A.E. Dummett (ed.) , Formal systems and recursive functions , North-Holland (1965) pp. 92–130 |
Kripke models. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kripke_models&oldid=14348