Cotangent
From Encyclopedia of Mathematics
One of the trigonometric functions:
 |
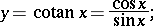other notations are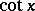 
, 
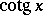and 
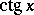. The domain of definition is the entire real line with the exception of the points with abscissas 
, 
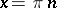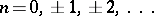. The cotangent is an unbounded odd periodic function (with period 
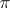). The cotangent and the tangent are related by
 |
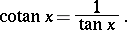The inverse function to the cotangent is called the arccotangent. The derivative of the cotangent is given by:
 |
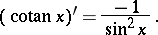The integral of the cotangent is given by:
 |
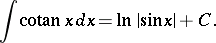The series expansion is:
 |
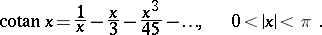The cotangent of a complex argument 
is a meromorphic function with poles at the points 
, 
.
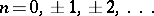Comments
See also Tangent, curve of the; Sine; Cosine.
How to Cite This Entry:
Cotangent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cotangent&oldid=14341
Cotangent. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cotangent&oldid=14341
This article was adapted from an original article by Yu.A. Gor'kov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article