Epidemic process
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A random process (cf. Stochastic process) that serves as a mathematical model of the spread of some epidemy. One of the simplest such models can be described as a continuous-time Markov process whose states at the moment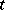 
are the number 
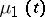of sick persons and the number 
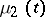of exposed persons. If 
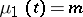and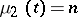 
, then at the time 
, 
, 
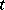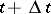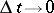, the transition probability is determined as follows: 
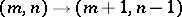with probability 
; 
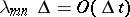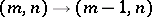with probability 
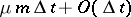. In this case the generating function
 |
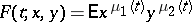satisfies the differential equation
 |
Comments
References
| [a1] | N.T.J. Bailey, "The mathematical theory of infections diseases and its applications" , Hafner (1975) |
| [a2] | D. Ludwig, "Stochastic population theories" , Springer (1974) |
How to Cite This Entry:
Epidemic process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epidemic_process&oldid=14259
Epidemic process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Epidemic_process&oldid=14259
This article was adapted from an original article by B.A. Sevast'yanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article