Stochastic differential
A random interval function  defined by the formula
defined by the formula
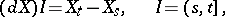 |
for every process  in the class of semi-martingales
in the class of semi-martingales  , with respect to a stochastic basis
, with respect to a stochastic basis  . In the family of stochastic differentials
. In the family of stochastic differentials  one introduces addition
one introduces addition  , multiplication by a process
, multiplication by a process  and the product operation
and the product operation  according to the following formulas:
according to the following formulas:

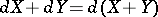 ;
;
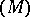
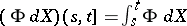 (a stochastic integral,
(a stochastic integral, 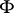 being a locally bounded predictable process which is adapted to the filtration
being a locally bounded predictable process which is adapted to the filtration  );
);
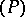
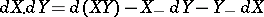 , where
, where 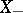 and
and 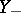 are the left-continuous versions of
are the left-continuous versions of 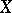 and
and  .
.
It then turns out that
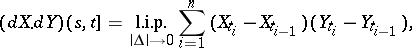 |
where 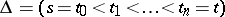 is an arbitrary decomposition of the interval
is an arbitrary decomposition of the interval 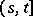 , l.i.p. is the limit in probability, and
, l.i.p. is the limit in probability, and 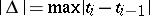 .
.
In stochastic analysis, the principle of "differentiation" of random functions, or Itô formula, is of importance: If 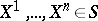 and the function
and the function 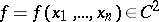 , then
, then
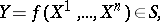 |
and
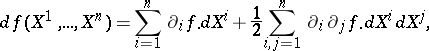 | (1) |
where 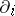 is the partial derivative with respect to the
is the partial derivative with respect to the 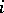 -th coordinate. In particular, it can be inferred from (1) that if
-th coordinate. In particular, it can be inferred from (1) that if 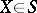 , then
, then
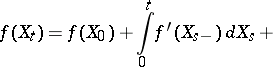 | (2) |
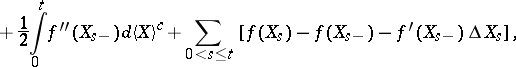 |
where 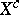 is the continuous martingale part of
is the continuous martingale part of 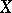 ,
, 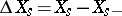 .
.
Formula (2) can be given the following form:
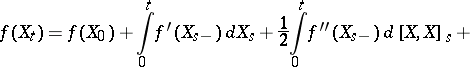 |
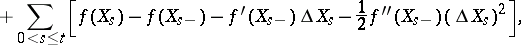 |
where 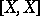 is the quadratic variation of
is the quadratic variation of 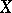 .
.
References
| [1] | K. Itô, S. Watanabe, "Introduction to stochastic differential equations" K. Itô (ed.) , Proc. Int. Symp. Stochastic Differential Equations Kyoto, 1976 , Wiley (1978) pp. I-XXX |
| [2] | I.I. Gikhman, A.V. Skorokhod, "Stochastic differential equations and their applications" , Kiev (1982) (In Russian) |
Comments
The product 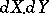 is more often written as
is more often written as 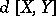 , where the so-called "square bracket"
, where the so-called "square bracket" 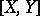 is the process with finite variation such that
is the process with finite variation such that 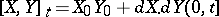 . When
. When 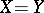 , one obtains the quadratic variation
, one obtains the quadratic variation 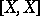 used at the end of the main article. Actually, it is a probabilistic quadratic variation: when
used at the end of the main article. Actually, it is a probabilistic quadratic variation: when 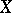 is a standard Brownian motion,
is a standard Brownian motion, 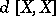 is the Lebesgue measure, but the true quadratic variation of the paths is almost surely infinite. See also Semi-martingale; Stochastic integral; Stochastic differential equation.
is the Lebesgue measure, but the true quadratic variation of the paths is almost surely infinite. See also Semi-martingale; Stochastic integral; Stochastic differential equation.
For the study of continuous-path processes evolving on non-flat manifolds the Itô stochastic differential is inconvenient, because the Itô formula (2) is incompatible with the ordinary rules of calculus relating different coordinate systems. A coordinate-free description can be obtained using the Stratonovich differential; see [a1], [a2], Chapt. 5, [a3], and Stratonovich integral.
References
| [a1] | K.D. Elworthy, "Stochastic differential equations on manifolds" , Cambridge Univ. Press (1982) |
| [a2] | N. Ikeda, S. Watanabe, "Stochastic differential equations and diffusion processes" , North-Holland (1989) pp. 97ff |
| [a3] | P.A. Meyer, "Geometrie stochastiques sans larmes" J. Azéma (ed.) M. Yor (ed.) , Sem. Probab. Strassbourg XV , Lect. notes in math. , 850 , Springer (1981) pp. 44–102 |
| [a4] | I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1988) |
| [a5] | L.C.G. Rogers, D. Williams, "Diffusion, Markov processes, and martingales" , 2. Itô calculus , Wiley (1987) |
| [a6] | S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Nonstandard methods in stochastic analysis and mathematical physics" , Acad. Press (1986) |
Stochastic differential. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_differential&oldid=14242