The polynomials 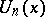 (cf. [a1] and [a4]) given by
(cf. [a1] and [a4]) given by
 | (a1) |
They reduce to the Fibonacci numbers 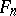 for
for 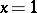 and they satisfy several identities, which may be easily proved by induction, e.g.:
and they satisfy several identities, which may be easily proved by induction, e.g.:
 | (a2) |
 | (a3) |
 | (a4) |
 | (a5) |
where
so that 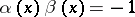 ; and
; and
 | (a6) |
where 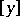 denotes the greatest integer in
denotes the greatest integer in 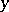 .
.
W.A. Webb and E.A. Parberry [a14] showed that the 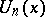 are irreducible polynomials over the ring of integers if and only if
are irreducible polynomials over the ring of integers if and only if  is a prime number (cf. also Irreducible polynomial). They also found that
is a prime number (cf. also Irreducible polynomial). They also found that 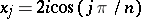 ,
, 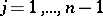 , are the
, are the 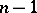 roots of
roots of 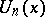 (see also [a2]). M. Bicknell [a1] proved that
(see also [a2]). M. Bicknell [a1] proved that 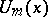 divides
divides 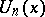 if and only if
if and only if 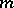 divides
divides  . V.E. Hoggatt Jr., and C.T. Long [a3] introduced the bivariate Fibonacci polynomials
. V.E. Hoggatt Jr., and C.T. Long [a3] introduced the bivariate Fibonacci polynomials 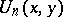 by the recursion
by the recursion
 | (a7) |
and they showed that the 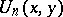 are irreducible over the rational numbers if and only if
are irreducible over the rational numbers if and only if  is a prime number. They also generalized (a5) and proved that
is a prime number. They also generalized (a5) and proved that
 | (a8) |
In a series of papers, A.N. Philippou and his associates (cf. [a5], [a6], [a7], [a8], [a9], [a10], [a11], [a12], [a13]) introduced and studied Fibonacci, Fibonacci-type and multivariate Fibonacci polynomials of order 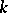 , and related them to probability and reliability. Let
, and related them to probability and reliability. Let 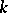 be a fixed positive integer greater than or equal to
be a fixed positive integer greater than or equal to  . The Fibonacci polynomials of order
. The Fibonacci polynomials of order 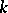 ,
, 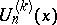 , are defined by
, are defined by
 | (a9) |
For 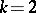 these reduce to
these reduce to 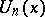 , and for
, and for 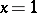 these reduce to
these reduce to 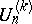 , the Fibonacci numbers of order
, the Fibonacci numbers of order 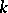 (cf. [a11]). Deriving and expanding the generating function of
(cf. [a11]). Deriving and expanding the generating function of 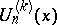 , they [a12] obtained the following generalization of (a6) in terms of the multinomial coefficients (cf. Multinomial coefficient):
, they [a12] obtained the following generalization of (a6) in terms of the multinomial coefficients (cf. Multinomial coefficient):
 | (a10) |
where the sum is taken over all non-negative integers  such that
such that 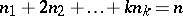 . They also obtained a simpler formula in terms of binomial coefficients. As a byproduct of (a10), they were able to relate these polynomials to the number of trials
. They also obtained a simpler formula in terms of binomial coefficients. As a byproduct of (a10), they were able to relate these polynomials to the number of trials 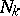 until the occurrence of the
until the occurrence of the 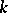 th consecutive success in independent trials with success probability
th consecutive success in independent trials with success probability  . For
. For 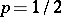 this formula reduces to
this formula reduces to
 | (a11) |
The Fibonacci-type polynomials of order 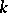 ,
, 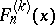 , defined by
, defined by
 | (a12) |
have simpler multinomial and binomial expansions than 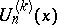 . The two families of polynomials are related by
. The two families of polynomials are related by
 | (a13) |
Furthermore, with 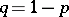 ,
,
 | (a14) |
Assuming that the components of a consecutive 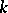 -out-of-
-out-of- :
: 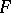 -system are ordered linearly and function independently with probability
-system are ordered linearly and function independently with probability 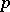 , Philippou [a6] found that the reliability of the system,
, Philippou [a6] found that the reliability of the system, 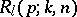 , is given by
, is given by
 | (a15) |
If the components of the system are ordered circularly, then its reliability, 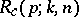 , is given by (cf. [a10])
, is given by (cf. [a10])
 | (a16) |
Next, denote by 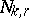 the number of independent trials with success probability
the number of independent trials with success probability 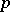 until the occurrence of the
until the occurrence of the  th
th 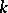 th consecutive success. It is well-known [a5] that
th consecutive success. It is well-known [a5] that 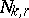 has the negative binomial distribution of order
has the negative binomial distribution of order 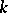 with parameters
with parameters  and
and 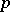 . Philippou and C. Georghiou [a9] have related this probability distribution to the
. Philippou and C. Georghiou [a9] have related this probability distribution to the 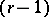 -fold convolution of
-fold convolution of 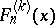 with itself, say
with itself, say 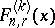 , as follows:
, as follows:
 | (a17) |
which reduces to (a14) for 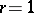 , and they utilized effectively relation (a17) for deriving two useful expressions, a binomial and a recurrence one, for calculating the above probabilities.
, and they utilized effectively relation (a17) for deriving two useful expressions, a binomial and a recurrence one, for calculating the above probabilities.
Let 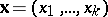 . The multivariate Fibonacci polynomials of order
. The multivariate Fibonacci polynomials of order 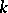 (cf. [a8]),
(cf. [a8]), 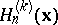 , are defined by the recurrence
, are defined by the recurrence
 | (a18) |
For 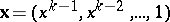 ,
, 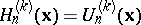 ,
, 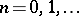 , and for
, and for 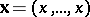 ,
, 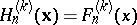 . These polynomials have the following multinomial expansion:
. These polynomials have the following multinomial expansion:
 | (a19) |
where the sum is taken over all non-negative integers  such that
such that 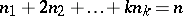 . Let the random variable
. Let the random variable 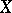 be distributed as a multi-parameter negative binomial distribution of order
be distributed as a multi-parameter negative binomial distribution of order 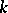 (cf. [a7]) with parameters
(cf. [a7]) with parameters 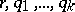 (
(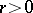 ,
, 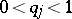 for
for 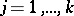 and
and 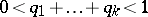 ). Philippou and D.L. Antzoulakos [a8] showed that the
). Philippou and D.L. Antzoulakos [a8] showed that the 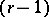 -fold convolution,
-fold convolution, 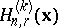 , of
, of 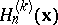 with itself is related to this distribution by
with itself is related to this distribution by
 | (a20) |
Furthermore, they have effectively utilized relation (a20) in deriving a recurrence for calculating the above probabilities.
References
| [a1] | M. Bicknell, "A primer for the Fibonacci numbers VII" Fibonacci Quart. , 8 (1970) pp. 407–420 |
| [a2] | V.E. Hoggatt Jr., M. Bicknell, "Roots of Fibonacci polynomials" Fibonacci Quart. , 11 (1973) pp. 271–274 |
| [a3] | V.E. Hoggatt Jr., C.T. Long, "Divisibility properties of generalized Fibonacci polynomials" Fibonacci Quart. , 12 (1974) pp. 113–120 |
| [a4] | E. Lucas, "Theorie de fonctions numeriques simplement periodiques" Amer. J. Math. , 1 (1878) pp. 184–240; 289–321 |
| [a5] | A.N. Philippou, "The negative binomial distribution of order 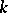 and some of its properties" Biom. J. , 26 (1984) pp. 789–794 and some of its properties" Biom. J. , 26 (1984) pp. 789–794 |
| [a6] | A.N. Philippou, "Distributions and Fibonacci polynomials of order 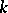 , longest runs, and reliability of concecutive- , longest runs, and reliability of concecutive- -out-of- -out-of- : : 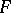 systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227 systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227 |
| [a7] | A.N. Philippou, "On multiparameter distributions of order 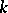 " Ann. Inst. Statist. Math. , 40 (1988) pp. 467–475 " Ann. Inst. Statist. Math. , 40 (1988) pp. 467–475 |
| [a8] | A.N. Philippou, D.L. Antzoulakos, "Multivariate Fibonacci polynomials of order 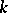 and the multiparameter negative binomial distribution of the same order" G.E. Bergum (ed.) A.N. Philippou (ed.) A.F. Horadam (ed.) , Applications of Fibonacci Numbers , 3 , Kluwer Acad. Publ. (1990) pp. 273–279 and the multiparameter negative binomial distribution of the same order" G.E. Bergum (ed.) A.N. Philippou (ed.) A.F. Horadam (ed.) , Applications of Fibonacci Numbers , 3 , Kluwer Acad. Publ. (1990) pp. 273–279 |
| [a9] | A.N. Philippou, C. Georghiou, "Convolutions of Fibonacci-type polynomials of order 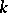 and the negative binomial distributions of the same order" Fibonacci Quart. , 27 (1989) pp. 209–216 and the negative binomial distributions of the same order" Fibonacci Quart. , 27 (1989) pp. 209–216 |
| [a10] | A.N. Philippou, F.S. Makri, "Longest circular runs with an application in reliability via the Fibonacci-type polynomials of order k" G.E. Bergum (ed.) A.N. Philippou (ed.) A.F. Horadam (ed.) , Applications of Fibonacci Numbers , 3 , Kluwer Acad. Publ. (1990) pp. 281–286 |
| [a11] | A.N. Philippou, A.A. Muwafi, "Waiting for the kth consecutive success and the Fibonacci sequence of order 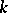 " Fibonacci Quart. , 20 (1982) pp. 28–32 " Fibonacci Quart. , 20 (1982) pp. 28–32 |
| [a12] | A.N. Philippou, C. Georghiou, G.N. Philippou, "Fibonacci polynomials of order 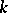 , multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550 , multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550 |
| [a13] | A.N. Philippou, C. Georghiou, G.N. Philippou, "Fibonacci-type polynomials of order 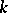 with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105 with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105 |
| [a14] | W.A. Webb, E.A. Parberry, "Divisibility properties of Fibonacci polynomials" Fibonacci Quart. , 7 (1969) pp. 457–463 |
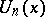 (cf. [a1] and [a4]) given by
(cf. [a1] and [a4]) given by

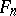 for
for 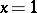 and they satisfy several identities, which may be easily proved by induction, e.g.:
and they satisfy several identities, which may be easily proved by induction, e.g.:




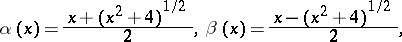
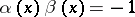 ; and
; and

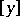 denotes the greatest integer in
denotes the greatest integer in 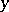 .
.
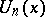 are irreducible polynomials over the ring of integers if and only if
are irreducible polynomials over the ring of integers if and only if  is a prime number (cf. also Irreducible polynomial). They also found that
is a prime number (cf. also Irreducible polynomial). They also found that 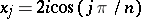 ,
, 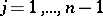 , are the
, are the 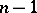 roots of
roots of 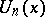 (see also [a2]). M. Bicknell [a1] proved that
(see also [a2]). M. Bicknell [a1] proved that 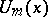 divides
divides 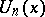 if and only if
if and only if 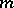 divides
divides  . V.E. Hoggatt Jr., and C.T. Long [a3] introduced the bivariate Fibonacci polynomials
. V.E. Hoggatt Jr., and C.T. Long [a3] introduced the bivariate Fibonacci polynomials 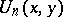 by the recursion
by the recursion

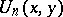 are irreducible over the rational numbers if and only if
are irreducible over the rational numbers if and only if  is a prime number. They also generalized (a5) and proved that
is a prime number. They also generalized (a5) and proved that

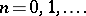
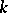 , and related them to probability and reliability. Let
, and related them to probability and reliability. Let 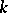 be a fixed positive integer greater than or equal to
be a fixed positive integer greater than or equal to  . The Fibonacci polynomials of order
. The Fibonacci polynomials of order 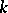 ,
, 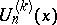 , are defined by
, are defined by

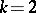 these reduce to
these reduce to 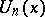 , and for
, and for 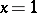 these reduce to
these reduce to 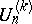 , the Fibonacci numbers of order
, the Fibonacci numbers of order 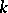 (cf. [a11]). Deriving and expanding the generating function of
(cf. [a11]). Deriving and expanding the generating function of 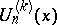 , they [a12] obtained the following generalization of (a6) in terms of the multinomial coefficients (cf. Multinomial coefficient):
, they [a12] obtained the following generalization of (a6) in terms of the multinomial coefficients (cf. Multinomial coefficient):

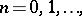
 such that
such that 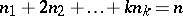 . They also obtained a simpler formula in terms of binomial coefficients. As a byproduct of (a10), they were able to relate these polynomials to the number of trials
. They also obtained a simpler formula in terms of binomial coefficients. As a byproduct of (a10), they were able to relate these polynomials to the number of trials 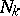 until the occurrence of the
until the occurrence of the 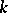 th consecutive success in independent trials with success probability
th consecutive success in independent trials with success probability  . For
. For 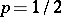 this formula reduces to
this formula reduces to

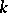 ,
, 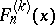 , defined by
, defined by

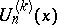 . The two families of polynomials are related by
. The two families of polynomials are related by

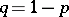 ,
,


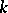 -out-of-
-out-of- :
: 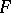 -system are ordered linearly and function independently with probability
-system are ordered linearly and function independently with probability 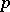 , Philippou [a6] found that the reliability of the system,
, Philippou [a6] found that the reliability of the system, 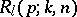 , is given by
, is given by


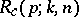 , is given by (cf. [a10])
, is given by (cf. [a10])

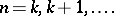
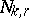 the number of independent trials with success probability
the number of independent trials with success probability 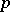 until the occurrence of the
until the occurrence of the  th
th 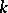 th consecutive success. It is well-known [a5] that
th consecutive success. It is well-known [a5] that 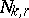 has the negative binomial distribution of order
has the negative binomial distribution of order 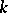 with parameters
with parameters  and
and 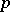 . Philippou and C. Georghiou [a9] have related this probability distribution to the
. Philippou and C. Georghiou [a9] have related this probability distribution to the 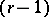 -fold convolution of
-fold convolution of 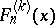 with itself, say
with itself, say 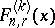 , as follows:
, as follows:

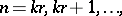
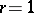 , and they utilized effectively relation (a17) for deriving two useful expressions, a binomial and a recurrence one, for calculating the above probabilities.
, and they utilized effectively relation (a17) for deriving two useful expressions, a binomial and a recurrence one, for calculating the above probabilities.
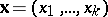 . The multivariate Fibonacci polynomials of order
. The multivariate Fibonacci polynomials of order 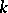 (cf. [a8]),
(cf. [a8]), 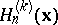 , are defined by the recurrence
, are defined by the recurrence

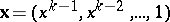 ,
, 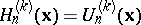 ,
, 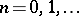 , and for
, and for 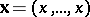 ,
, 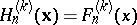 . These polynomials have the following multinomial expansion:
. These polynomials have the following multinomial expansion:

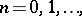
 such that
such that 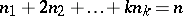 . Let the random variable
. Let the random variable 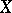 be distributed as a multi-parameter negative binomial distribution of order
be distributed as a multi-parameter negative binomial distribution of order 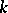 (cf. [a7]) with parameters
(cf. [a7]) with parameters 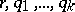 (
(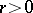 ,
, 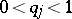 for
for 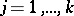 and
and 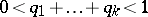 ). Philippou and D.L. Antzoulakos [a8] showed that the
). Philippou and D.L. Antzoulakos [a8] showed that the 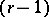 -fold convolution,
-fold convolution, 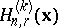 , of
, of 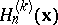 with itself is related to this distribution by
with itself is related to this distribution by

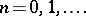
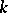 and some of its properties" Biom. J. , 26 (1984) pp. 789–794
and some of its properties" Biom. J. , 26 (1984) pp. 789–794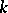 , longest runs, and reliability of concecutive-
, longest runs, and reliability of concecutive- -out-of-
-out-of- :
: 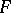 systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227
systems" A.N. Philippou (ed.) G.E. Bergum (ed.) A.F. Horadam (ed.) , Fibonacci Numbers and Their Applications , Reidel (1986) pp. 203–227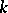 " Ann. Inst. Statist. Math. , 40 (1988) pp. 467–475
" Ann. Inst. Statist. Math. , 40 (1988) pp. 467–475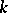 and the multiparameter negative binomial distribution of the same order" G.E. Bergum (ed.) A.N. Philippou (ed.) A.F. Horadam (ed.) , Applications of Fibonacci Numbers , 3 , Kluwer Acad. Publ. (1990) pp. 273–279
and the multiparameter negative binomial distribution of the same order" G.E. Bergum (ed.) A.N. Philippou (ed.) A.F. Horadam (ed.) , Applications of Fibonacci Numbers , 3 , Kluwer Acad. Publ. (1990) pp. 273–279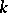 and the negative binomial distributions of the same order" Fibonacci Quart. , 27 (1989) pp. 209–216
and the negative binomial distributions of the same order" Fibonacci Quart. , 27 (1989) pp. 209–216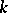 " Fibonacci Quart. , 20 (1982) pp. 28–32
" Fibonacci Quart. , 20 (1982) pp. 28–32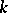 , multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550
, multinomial expansions and probability" Internat. J. Math. Math. Sci. , 6 (1983) pp. 545–550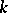 with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105
with probability applications" Fibonacci Quart. , 23 (1985) pp. 100–105