Structure
A synonym for algebraic system. Similarly, substructure is a synonym for "subsystem" , and elementary substructure is a synonym for "elementary subsystem" (cf. Model theory). If  is a first-order language of signature
is a first-order language of signature  and
and  is an algebraic system of signature
is an algebraic system of signature  , then
, then  is called an
is called an  -structure.
-structure.
A first-order language  is uniquely determined by its signature
is uniquely determined by its signature  (cf. Algebraic system). Therefore, in a more informal way of writing, many authors describe
(cf. Algebraic system). Therefore, in a more informal way of writing, many authors describe 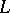 by just giving the set
by just giving the set 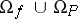 of function symbols (also called "functionals" ) and relation symbols (also called "predicates" ). Here, one omits the mapping
of function symbols (also called "functionals" ) and relation symbols (also called "predicates" ). Here, one omits the mapping  , which assigns to every symbol its arity, that is, the number of variables of the function or relation which interprets the symbol in a structure. This is justified when the arity can be read off from the symbol by convention. It is even common to write
, which assigns to every symbol its arity, that is, the number of variables of the function or relation which interprets the symbol in a structure. This is justified when the arity can be read off from the symbol by convention. It is even common to write 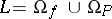 . For example,
. For example, 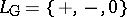 is called the language of groups (additively written),
is called the language of groups (additively written), 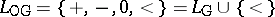 is the language of ordered groups,
is the language of ordered groups,  is the language of rings with
is the language of rings with  , and
, and  is the language of ordered rings. Here, "+" and "" are binary function symbols, "-" is a unary function symbol (for additive inversion), "<" is a binary relation symbol, and "0" and "1" are constant symbols. A constant symbol, belonging to
is the language of ordered rings. Here, "+" and "" are binary function symbols, "-" is a unary function symbol (for additive inversion), "<" is a binary relation symbol, and "0" and "1" are constant symbols. A constant symbol, belonging to 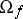 , is a
, is a  -ary function symbol, but often constant symbols are considered separately. The field axioms can be formulated in the language of rings, but one can also use the language of fields obtained from
-ary function symbol, but often constant symbols are considered separately. The field axioms can be formulated in the language of rings, but one can also use the language of fields obtained from  by adjoining a unary function symbol for multiplicative inversion.
by adjoining a unary function symbol for multiplicative inversion.
If the language  is given by a set of relation symbols, function symbols and constant symbols, then an
is given by a set of relation symbols, function symbols and constant symbols, then an 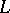 -structure
-structure 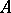 is a set
is a set 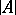 , called the universe of the structure
, called the universe of the structure 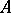 , together with relations and functions on
, together with relations and functions on  and elements of
and elements of 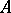 (constants) which interpret the corresponding symbols of
(constants) which interpret the corresponding symbols of 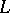 . Often,
. Often, 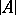 is identified with
is identified with 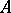 ; for example,
; for example,  may denote the set of real numbers as well as the field of real numbers. In this spirit, an element of
may denote the set of real numbers as well as the field of real numbers. In this spirit, an element of 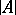 is also called an element of
is also called an element of 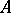 , and the cardinality of a structure is defined to be the cardinality of its universe.
, and the cardinality of a structure is defined to be the cardinality of its universe.
If 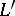 is a language containing
is a language containing 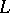 (as sets of symbols) and
(as sets of symbols) and 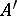 is an
is an 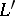 -structure such that
-structure such that 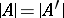 and the interpretations of the relation, function and constant symbols of
and the interpretations of the relation, function and constant symbols of 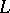 are the same in
are the same in 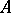 as in
as in  , then
, then  is called an expansion of
is called an expansion of 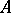 , and
, and  is called a reduct of
is called a reduct of  . For example, a field is an expansion of the underlying additive group, and this group is a reduct of the field.
. For example, a field is an expansion of the underlying additive group, and this group is a reduct of the field.
If 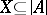 , then to add a name for every element in
, then to add a name for every element in 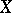 to the language, one passes to the expansion
to the language, one passes to the expansion  of
of 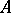 , which has signature
, which has signature  (cf. Model theory; Elimination of quantifiers).
(cf. Model theory; Elimination of quantifiers).
Structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Structure&oldid=14175