Chetaev function
A function 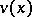 , defined in a neighbourhood of a fixed point
, defined in a neighbourhood of a fixed point 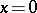 of a system of ordinary differential equations
of a system of ordinary differential equations
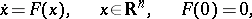 | (*) |
and satisfying the two conditions: 1) there exists a domain 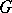 with the point
with the point 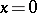 on its boundary in which
on its boundary in which 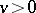 , and
, and 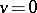 on the boundary of the domain close to
on the boundary of the domain close to 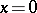 ; and 2) in
; and 2) in 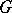 the derivative along the flow of the system (*) (cf. Differentiation along the flow of a dynamical system) satisfies
the derivative along the flow of the system (*) (cf. Differentiation along the flow of a dynamical system) satisfies 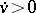 .
.
Chetaev's theorem [1] holds: If there is a Chetaev function  for the system (*), then the fixed point
for the system (*), then the fixed point 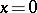 is Lyapunov unstable.
is Lyapunov unstable.
A Chetaev function is a generalization of a Lyapunov function and gives a convenient way of proving instability (cf. [2]). For example, for the system
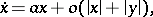 |
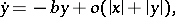 |
where  , a Chetaev function is
, a Chetaev function is  for any
for any 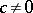 . Generalizations of Chetaev functions have been suggested, in particular for non-autonomous systems (cf. [3]).
. Generalizations of Chetaev functions have been suggested, in particular for non-autonomous systems (cf. [3]).
References
| [1] | N.G. Chetaev, "A theorem on instability" Dokl. Akad. Nauk SSSR , 1 : 9 (1934) pp. 529–531 (In Russian) |
| [2] | N.G. Chetaev, "Stability of motion" , Moscow (1965) (In Russian) |
| [3] | N.N. Krasovskii, "Stability of motion. Applications of Lyapunov's second method to differential systems and equations with delay" , Stanford Univ. Press (1963) (Translated from Russian) |
| [4] | N. Rouche, P. Habets, M. Laloy, "Stability theory by Liapunov's direct method" , Springer (1977) |
Chetaev function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chetaev_function&oldid=14071