Weak singularity
polar singularity
The unboundedness of an integral kernel 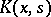 (cf. Kernel of an integral operator) when the product
(cf. Kernel of an integral operator) when the product 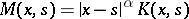 ,
, 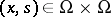 , is bounded. Here,
, is bounded. Here,  is a set in the space
is a set in the space 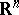 ,
, 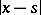 is the distance between two points
is the distance between two points  and
and  and
and 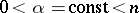 . The integral operator generated by such a kernel,
. The integral operator generated by such a kernel,
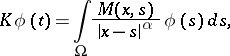 | (1) |
is called an integral operator with a weak singularity (or with a polar singularity). Let  be a compact subset of
be a compact subset of 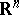 . If
. If  is continuous on
is continuous on 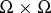 , the operator (1) is completely continuous (cf. Completely-continuous operator) on the space of continuous functions
, the operator (1) is completely continuous (cf. Completely-continuous operator) on the space of continuous functions 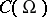 , and if
, and if 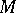 is bounded, then the operator (1) is completely continuous on the space
is bounded, then the operator (1) is completely continuous on the space 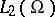 .
.
The kernel
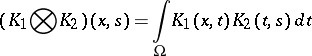 | (2) |
is called the convolution of the kernels 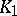 and
and  . Suppose
. Suppose 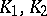 have weak singularities, with
have weak singularities, with
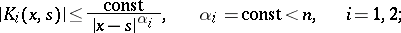 |
then their convolution (2) is bounded or has a weak singularity, and:
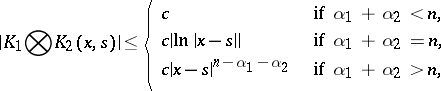 |
where  is a constant.
is a constant.
If a kernel has a weak singularity, then all its iterated kernels from some iteration onwards are bounded.
References
| [1] | V.I. Smirnov, "A course of higher mathematics" , 5 , Addison-Wesley (1964) (Translated from Russian) |
| [2] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [3] | M.A. Krasnosel'skii, et al., "Integral operators in spaces of summable functions" , Noordhoff (1976) (Translated from Russian) |
Comments
Weakly-singular kernels appear frequently in the boundary integral equation method for solving elliptic equations (see [a1]). Another important integral equation with a weakly-singular kernel is the Abel integral equation ([a2]).
References
| [a1] | D.L. Colton, R. Kress, "Integral equation methods in scattering theory" , Wiley (1983) |
| [a2] | R. Gorenflo, S. Vessella, "Abel integral equations in analysis and applications" , Springer (1991) |
| [a3] | P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) pp. Sects. I.1.2; II.6 (Translated from Russian) |
| [a4] | H. Hochstadt, "Integral equations" , Wiley (1975) pp. Sect. II.4 |
Weak singularity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_singularity&oldid=14001