Lyapunov-Schmidt equation

A non-linear integral equation of the form

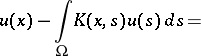(1)

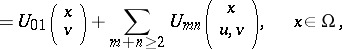where

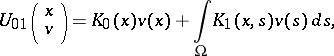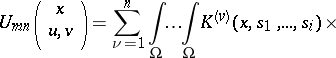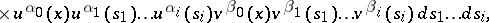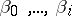, are non-negative integers,

is a closed bounded set in a finite-dimensional Euclidean space, and the function 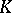are given continuous functions of their arguments, 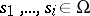, and is the unknown function. The sum on the right-hand side of (1) may be finite or it may represent an infinite series. In the latter case the series is called an integro-power series of two functional arguments. It is assumed that the series converges absolutely and uniformly.

If 1 is not a characteristic number of the kernel 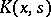, then equation (1) has a unique small solution in the class of continuous functions for sufficiently small 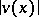. This solution can be represented as an integro-power series. The case when 1 is a characteristic number of the kernel 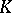is more complicated. In this case one constructs a system of equations — the branching equations (bifurcation equations):

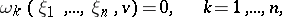(2)

where 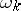are known power series and is the multiplicity of the characteristic number 1. In the general case the system (2) has a non-unique solution. Whatever the fixed sufficiently small function , to every small continuous solution of (2) (a continuous solution of (2) is said to be small if 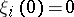) there corresponds a small solution of (1) that can be represented as an integro-power series.

An equation of the type (1) was first considered by A.M. Lyapunov in 1906, and later — in a more general form — by E. Schmidt in 1908.

References

[1]	M.M. Vainberg, V.A. Trenogin, "Theory of branching of solutions of non-linear equations" , Noordhoff (1974) (Translated from Russian)
[2]	N.S. Smirnov, "Introduction to the theory of integral equations" , Moscow-Leningrad (1936) (In Russian)

References

[a1]	S.-N. Chow, J.K. Hale, "Methods of bifurcation theory" , Springer (1982)