Suzuki-2-group
From Encyclopedia of Mathematics
A finite non-Abelian  -group
-group 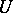 , other than the group of quaternions, which admits a cyclic group of automorphisms
, other than the group of quaternions, which admits a cyclic group of automorphisms 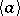 that acts transitively on the set
that acts transitively on the set  of elements of order 2 of
of elements of order 2 of 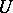 . This means that for any two elements
. This means that for any two elements  and
and 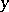 of
of  there is a natural number
there is a natural number  such that
such that 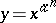 . In the Suzuki
. In the Suzuki  -group
-group 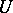 , the set
, the set  and the identity element constitute a subgroup
and the identity element constitute a subgroup 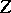 that coincides with the centre of
that coincides with the centre of 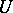 ; the quotient group
; the quotient group 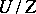 is then elementary Abelian. If the order of
is then elementary Abelian. If the order of 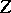 is equal to
is equal to 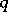 , then the order of
, then the order of 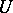 is equal to
is equal to 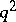 or
or 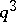 .
.
Suzuki  -groups have been fully described (see [1]). The name derives from the fact that in a Suzuki group, the Sylow
-groups have been fully described (see [1]). The name derives from the fact that in a Suzuki group, the Sylow  -group
-group 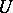 has these properties.
has these properties.
References
| [1] | G. Higman, "Suzuki 2-groups" Ill. J. Math. , 7 : 1 (1963) pp. 79–96 |
How to Cite This Entry:
Suzuki-2-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Suzuki-2-group&oldid=13964
Suzuki-2-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Suzuki-2-group&oldid=13964
This article was adapted from an original article by V.D. Mazurov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article