Co-H-space
A topological space with a co-multiplication; the dual notion is an 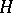 -space.
-space.
Comments
The sum of two objects 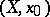 and
and 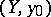 in the category of pointed topological spaces is the disjoint union of
in the category of pointed topological spaces is the disjoint union of 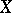 and
and 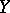 with
with 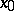 and
and 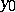 identified, and this point serves as base point; it can be realized (and visualized) as the subset
identified, and this point serves as base point; it can be realized (and visualized) as the subset 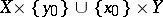 of
of 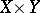 . A co-
. A co-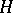 -space thus is a pointed topological space with a continuous mapping of pointed spaces
-space thus is a pointed topological space with a continuous mapping of pointed spaces 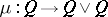 , termed co-multiplication, such that the composites
, termed co-multiplication, such that the composites  and
and 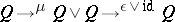 are homotopic to the identity. Here
are homotopic to the identity. Here  is the mapping which sends all of
is the mapping which sends all of 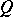 to the base point
to the base point 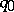 . If the two composites
. If the two composites 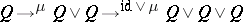 and
and 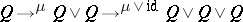 are homotopic to each other, the co-multiplication is called homotopy co-associative (or homotopy associative). A continuous mapping of pointed spaces
are homotopic to each other, the co-multiplication is called homotopy co-associative (or homotopy associative). A continuous mapping of pointed spaces 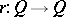 is a homotopy co-inverse for
is a homotopy co-inverse for 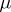 if the two composites
if the two composites 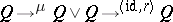 and
and 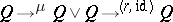 are both homotopic to
are both homotopic to 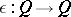 . Here for
. Here for 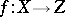 ,
, 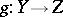 ,
, 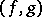 is the mapping determined by the defining property of the sum in the category of pointed topological spaces, i.e.
is the mapping determined by the defining property of the sum in the category of pointed topological spaces, i.e.  restricted to
restricted to 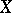 is equal to
is equal to 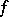 , and
, and 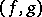 restricted to
restricted to 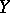 is equal to
is equal to 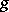 . A co-
. A co-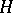 -space with co-associative co-multiplication which admits a homotopy co-inverse is called an
-space with co-associative co-multiplication which admits a homotopy co-inverse is called an 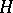 -co-group. Thus, an
-co-group. Thus, an 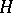 -co-group is a co-group object in the category
-co-group is a co-group object in the category 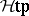 of pointed topological spaces and homotopy classes of mappings.
of pointed topological spaces and homotopy classes of mappings.
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. I, Sect. 6 |
Co-H-space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Co-H-space&oldid=13962