Cartesian factorization
From Encyclopedia of Mathematics
(in topology)
A factorization of a space into a topological product. An important problem on non-trivial Cartesian factorizations concerns the cubes 
and the Euclidean spaces 
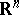. For instance, if a space 
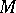is obtained from 
, 
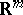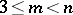, by identifying the points of an arc 
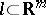for which 
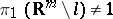(cf. Wild imbedding), then 
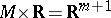and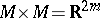 
. Any smooth compact contractible manifold 
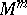is a factor of an 
, 
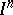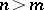. Any factor of 
, 
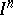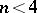, is an 
, 
.
References
| [1] | Itogi Nauk. Algebra. Topol. Geom. 1965 (1967) pp. 227; 243 |
Comments
Another famous example is Bing's "Dog Bone" decomposition of 
-dimensional Euclidean space, its product with a line is homeomorphic to 
-dimensional Euclidean space.
References
| [a1] | R.H. Bing, "The cartesian product of a certain non-manifold and a line is 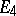 ," Ann. of Math. , 70 (1959) pp. 399–412 |
| [a2] | R.J. Daverman, "Decompositions of manifolds" , Acad. Press (1986) |
How to Cite This Entry:
Cartesian factorization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartesian_factorization&oldid=13939
Cartesian factorization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cartesian_factorization&oldid=13939
This article was adapted from an original article by A.V. Chernavskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article