Connes-Moscovici index theorem

Gamma index theorem, index theorem

A theorem [a3] which computes the pairing of a cyclic cocycle of the group algebra with the algebraic -theory index of an invariant (pseudo-) differential operator on a covering with Galois group (or group of deck transformations) (cf. also Cohomology).

The ingredients of this theorem are stated in more detail below. Let be a smooth compact manifold.

First, any -invariant, elliptic partial differential operator (cf. Elliptic partial differential equation) on 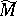has an algebraic -theory index . The definition of is obtained using the boundary mapping on applied to 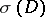, the principal symbol of 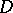(cf. also Symbol of an operator). This gives

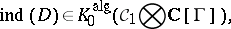where 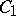is the algebra of trace-class operators on 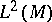(cf. also Trace). More generally, one can assume that 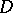is an invariant pseudo-differential operator on 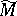(with nice support).

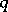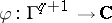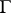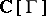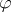Secondly, it is known [a2] that any group-cohomology -cocycle of can be represented by an anti-symmetric function, and hence it defines a cyclic cocycle on the group algebra of the group . Moreover, the class of this cocycle in the periodic cyclic cohomology group , also denoted by , depends only on the class of 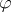in . Here, as customary, denotes the classifying space of , whose simplicial cohomology is known to be isomorphic to 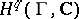, the group cohomology of .

Finally, any element 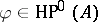gives rise to a group morphism , see [a2]. In particular, any group cocycle gives rise to a mapping

using also the trace on .

The Connes–Moscovici index theorem now states [a3]): Let 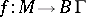be the mapping classifying the covering , let 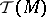be the Todd class of 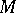, and let be the Chern character of the element in defined by 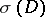, as in the Atiyah–Singer index theorem (see [a1] and Index formulas). Then

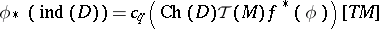is a pairing of a compactly supported cohomology class with the fundamental class of . Here, .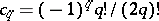

The Connes–Moscovici index theorem is sometimes called the higher index theorem for coverings and is the prototype of a higher index theorem.

References

[a1]	M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" Ann. of Math. , 93 (1971) pp. 484–530
[a2]	A. Connes, "Non-commutative differential geometry" Publ. Math. IHES , 62 (1985) pp. 41–144
[a3]	A. Connes, H. Moscovici, "Cyclic cohomology, the Novikov conjecture and hyperbolic groups" Topology , 29 (1990) pp. 345–388
[a4]	G. Lusztig, "Novikov's higher signature and families of elliptic operators" J. Diff. Geom. , 7 (1972) pp. 229–256