Remainder of an integer
 modulo
modulo  , residue of
, residue of  modulo
modulo 
Any integer  which is congruent to
which is congruent to  modulo
modulo  (cf. Congruence). Let
(cf. Congruence). Let  be the remainder of division of
be the remainder of division of  by some integer
by some integer 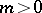 ,
, 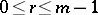 ; then the residue
; then the residue 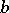 of the number
of the number  modulo
modulo  will have the form
will have the form 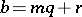 , where
, where 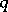 is some integer. The residue corresponding to
is some integer. The residue corresponding to  is equal to
is equal to  and is called the least non-negative residue of
and is called the least non-negative residue of  . The smallest (in absolute value) residue
. The smallest (in absolute value) residue 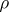 is called the absolutely smallest residue of
is called the absolutely smallest residue of  . If
. If 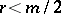 , then
, then 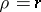 ; if
; if 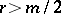 , then
, then 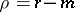 ; finally, if
; finally, if 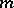 is even and
is even and 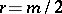 , either
, either 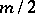 or
or 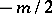 may be taken as
may be taken as 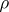 .
.
A system consisting of 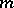 integers each one of which is the residue of one and only one of the numbers
integers each one of which is the residue of one and only one of the numbers  is called a complete system of residues modulo
is called a complete system of residues modulo  . The smallest non-negative residues
. The smallest non-negative residues  or the absolutely smallest residues are the complete systems of residues which are most frequently used.
or the absolutely smallest residues are the complete systems of residues which are most frequently used.
A power residue of degree  modulo
modulo 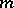 ,
,  , is any integer
, is any integer  , coprime with
, coprime with 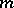 , for which the congruence
, for which the congruence
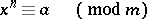 |
is solvable. If this congruence is not solvable,  is called a power non-residue of degree
is called a power non-residue of degree  modulo
modulo 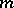 . In particular, if
. In particular, if  , the residues or non-residues are called quadratic; if
, the residues or non-residues are called quadratic; if 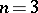 , they are called cubic; if
, they are called cubic; if  , they are called biquadratic (see also Power residue).
, they are called biquadratic (see also Power residue).
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XIII |
Remainder of an integer. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Remainder_of_an_integer&oldid=13893