Canonical imbedding

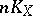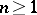An imbedding of an algebraic variety into a projective space using a multiple of the canonical class (see Linear system). Let be a non-singular projective curve of genus ; a mapping defined by the class is an imbedding for some provided that . Here one can take for non-hyper-elliptic curves, 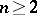for hyper-elliptic curves of genus 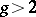and for curves of genus 2. These results have been used for the classification of algebraic curves of genus (see Canonical curve).

Similar questions have been considered for varieties of dimension greater than one, mainly surfaces. In this connection, the role of curves of genus is played by surfaces for which some multiple 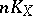of the canonical class gives a birational mapping of the surface onto its image in projective space. They are called surfaces of general type; the main result concerning these surfaces is the fact that for them, the class 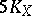already determines a regular mapping into a projective space which is a birational mapping. For example, a non-singular surface of degree 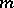in is a surface of general type if 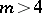. In this case the canonical class 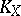itself gives a birational mapping. 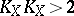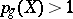If and (here 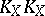is the self-intersection index and 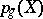is the geometric genus), then one can replace 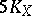by . 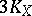Surfaces for which no multiple 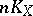gives an imbedding are divided into the following five families: rational surfaces, ruled surfaces, Abelian varieties, 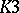-surfaces, and surfaces with a pencil of elliptic curves. In this connection, the rational and ruled surfaces are analogues of rational curves, while the remaining three families are analogues of elliptic curves.

The first generalizations of these results to higher-dimensional varieties appeared in [5].

References

[1]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)
[2]	F. Severi, "Vorlesungen über algebraische Geometrie" , Teubner (1921) (Translated from Italian)
[3]	"Algebraic surfaces" Trudy Mat. Inst. Steklov. , 75 (1965) (In Russian)
[4]	D. Husemoller, "Classification and embeddings of surfaces" R. Hartshorne (ed.) , Algebraic geometry (Arcata, 1974) , Proc. Symp. Pure Math. , 29 , Amer. Math. Soc. (1982) pp. 329–420
[5]	K. Ueno, "Introduction to classification theory of algebraic varieties and compact complex spaces" , Lect. notes in math. , 412 , Springer (1974) pp. 288–332

Comments

Let 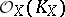be the line bundle, the canonical bundle, defined by a divisor representing 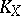(cf. Divisor). The mapping defined by its global sections 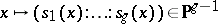is called the canonical mapping. (Here 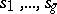are a basis of 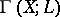and it is assumed that for all there is an 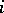with 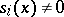, cf. Linear system.) Correspondingly, if 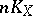is used instead of 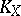, one speaks of a multi-canonical mapping and, if it is an imbedding, of a multi-canonical imbedding.

References

[a1]	K. Ueno, "Classification theory of algebraic varieties and compact complex spaces" , Springer (1975)
[a2]	S. Iitaka, "Algebraic geometry, an introduction to birational geometry of algebraic varieties" , Springer (1982)
[a3]	A. van de Ven, "Compact complex surfaces" , Springer (1984)
[a4]	E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1985)
[a5]	P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978)