Lens space
A manifold of odd dimension that arises as the orbit space of the isometric free action of a cyclic group  on the sphere
on the sphere  (cf. Action of a group on a manifold). It is convenient to take for
(cf. Action of a group on a manifold). It is convenient to take for  the unit sphere in the complex space
the unit sphere in the complex space  in which a basis is fixed. Suppose that
in which a basis is fixed. Suppose that  acts on each coordinate
acts on each coordinate  by multiplying it by
by multiplying it by  , where
, where  is invertible modulo
is invertible modulo 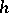 , that is, there are numbers
, that is, there are numbers 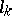 such that
such that  (
( ). This specifies an isometric free (thanks to the condition that
). This specifies an isometric free (thanks to the condition that  is invertible
is invertible  ) action of
) action of  on
on  , and any such action has this form described in a suitable coordinate system. The Reidemeister torsion corresponding to an
, and any such action has this form described in a suitable coordinate system. The Reidemeister torsion corresponding to an 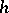 -th root of unity
-th root of unity  is defined for a lens space
is defined for a lens space 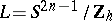 constructed in this way by the formula
constructed in this way by the formula  . Any piecewise-linear lens space
. Any piecewise-linear lens space 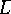 homeomorphic to it must have equal (up to
homeomorphic to it must have equal (up to  ) torsion, and it turns out that the sets of numbers
) torsion, and it turns out that the sets of numbers 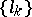 and
and  must coincide. Thus, these sets characterize lens spaces uniquely up to a piecewise-linear homeomorphism and even up to an isometry; on the other hand, by the topological invariance of the torsion, they also characterize lens spaces uniquely up to a homeomorphism. A lens space is aspherical up to dimension
must coincide. Thus, these sets characterize lens spaces uniquely up to a piecewise-linear homeomorphism and even up to an isometry; on the other hand, by the topological invariance of the torsion, they also characterize lens spaces uniquely up to a homeomorphism. A lens space is aspherical up to dimension  (that is,
(that is,  ,
,  ), and the fundamental group is equal to
), and the fundamental group is equal to  in view of the fact that the sphere
in view of the fact that the sphere 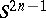 is the universal covering for
is the universal covering for  . The homology of
. The homology of  coincides up to dimension
coincides up to dimension  with the homology of the group
with the homology of the group 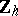 , that is, it is equal to
, that is, it is equal to  in all dimensions from
in all dimensions from  to
to 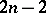 and
and 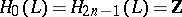 . The direct limit of the spaces
. The direct limit of the spaces  gives an Eilenberg–MacLane space of type
gives an Eilenberg–MacLane space of type  . Two lens spaces are homotopy equivalent if and only if the linking coefficients (cf. Linking coefficient)
. Two lens spaces are homotopy equivalent if and only if the linking coefficients (cf. Linking coefficient)  coincide, where
coincide, where  is a generator of the two-dimensional cohomology group. By means of these invariants one can establish the existence of asymmetric manifolds among lens spaces.
is a generator of the two-dimensional cohomology group. By means of these invariants one can establish the existence of asymmetric manifolds among lens spaces.
In the three-dimensional case lens spaces coincide with manifolds that have a Heegaard diagram of genus 1, and so they are Seifert manifolds (cf. Seifert manifold). It is convenient to represent the fundamental domain of the action of 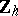 on
on  as a "lens" , i.e. the union of a spherical segment and its mirror image; this is how the name lens surface arose.
as a "lens" , i.e. the union of a spherical segment and its mirror image; this is how the name lens surface arose.
References
| [1] | H. Poincaré, , Selected work , 2 , Moscow (1972) pp. 728 (In Russian) |
| [2] | G. de Rham, "Sur la théorie des intersections et les intégrales multiples" Comm. Math. Helv. , 4 (1932) pp. 151–154 |
| [3] | H. Seifert, W. Threlfall, "A textbook of topology" , Acad. Press (1980) (Translated from German) |
| [4] | J.W. Milnor, O. Burlet, "Torsion et type simple d'homotopie" A. Haefliger (ed.) R. Narasimhan (ed.) , Essays on topology and related topics (Coll. Geneve, 1969) , Springer (1970) pp. 12–17 |
Lens space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lens_space&oldid=13837