Two-point tensor
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A tensor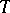 
which depends on a pair of points 
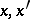in a manifold 
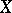, i.e. a tensor field 
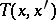defined on the product 
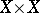. As an example, covariant derivatives of the world function 
and, in general, of an arbitrary invariant depending on two points are two-point tensors. The properties of such a tensor, in particular the limits of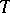 
and its derivatives as 
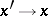, such as
 |
are employed in the calculus of variations and in the theory of relativity.
References
| [1] | J.L. Synge, "Relativity: the general theory" , North-Holland & Interscience (1960) |
How to Cite This Entry:
Two-point tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-point_tensor&oldid=13796
Two-point tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-point_tensor&oldid=13796
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article