Pfaffian form
A differential form of degree 1.
Comments
A Pfaffian form  defined on an open subset
defined on an open subset 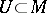 ,
,  a manifold, is of odd class
a manifold, is of odd class 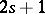 at
at  if it satisfies
if it satisfies
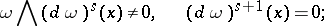 |
it is of even class  at
at  if it satisfies
if it satisfies
 |
Pfaffian forms of class 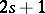 and
and 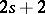 both define a Pfaffian equation of class
both define a Pfaffian equation of class 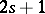 .
.
Darboux's theorem on Pfaffian forms says the following.
1) If 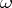 is a Pfaffian form of constant class
is a Pfaffian form of constant class 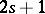 on an open subset
on an open subset 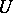 of a manifold
of a manifold 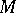 , then for every
, then for every 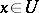 there is a neighbourhood
there is a neighbourhood 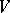 with a family of independent functions
with a family of independent functions 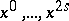 , such that on
, such that on 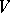 ,
,
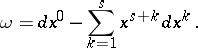 |
2) If 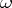 is a Pfaffian form of constant class
is a Pfaffian form of constant class 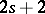 on an open subset
on an open subset 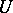 of a manifold
of a manifold 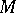 , then for every
, then for every 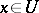 there is a neighbourhood
there is a neighbourhood 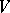 with a family of independent functions
with a family of independent functions 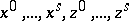 such that on
such that on 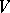 ,
,
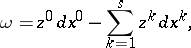 |
where the function 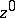 is without zeros on
is without zeros on 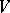 .
.
Thus, if 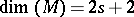 , the functions
, the functions 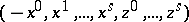 are canonical coordinates for the symplectic form
are canonical coordinates for the symplectic form 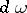 .
.
References
| [a1] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) pp. Chapt. V (Translated from French) |
Pfaffian form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pfaffian_form&oldid=13779