Locally trivial fibre bundle
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A fibre bundle (cf. Fibre space)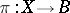 
with fibre 
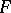such that for any point of the base 
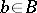there is a neighbourhood 
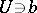and a homeomorphism 
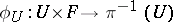such that 
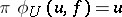, where 
, 
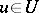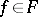. The mapping 
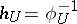is called a chart of the locally trivial bundle. The totality of charts 
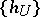associated with a covering of the base 
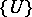forms the atlas of the locally trivial bundle. For example, a principal fibre bundle with a locally compact space and a Lie group 
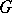is a locally trivial fibre bundle, and any chart 
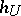satisfies the relation
 |
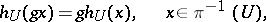where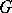 
acts on 
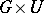according to the formula 
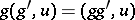. For any locally trivial fibre bundle 
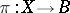and continuous mapping 
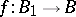the induced fibre bundle is locally trivial.
References
| [1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [2] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
| [3] | S.-T. Hu, "Homotopy theory" , Acad. Press (1959) |
| [4] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
How to Cite This Entry:
Locally trivial fibre bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_trivial_fibre_bundle&oldid=13769
Locally trivial fibre bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Locally_trivial_fibre_bundle&oldid=13769
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article