Dirac algebra

The Dirac algebra arises from Dirac's solution [a3] to the relativistic electron equation:

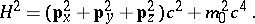Dirac found hypercomplex elements , , and (cf. also Hypercomplex number) such that

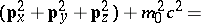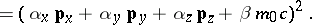The Hamiltonian is given, after the usual substitutions for the linear momentum components, by

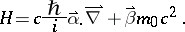The time-dependent equation is known as Dirac's equation:

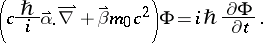The elements , , and 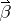satisfy and the anti-commutativity relations:

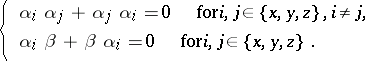The Dirac representation of the matrices 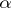and is

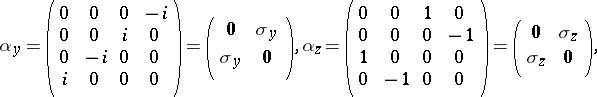where , 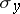and 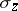are the Pauli spin matrices (cf. also Pauli matrices; Dirac matrices). This choice is not unique; pre-multiplying by any unitary matrix 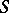and post-multiplying by 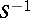will produce a new set of matrices satisfying the conditions. The defining relations are often expressed more abstractly by the Dirac gamma matrices

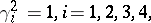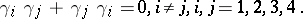The Dirac algebra is the 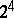-dimensional complex Clifford algebra generated by the gamma matrices under the usual matrix operations and is isomorphic to 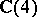, the ring of four-by-four matrices over the complex numbers 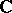. The use of the complex numbers as scalars apparently is motivated by the fact that complex numbers are use to express solutions to the Schrödinger wave equations (cf. also Schrödinger equation).

Two other "Dirac algebras" commonly appear in the literature [a4]; in each the relation among the squares of the generating elements, the metric, has been modified and the scalar field is the real numbers. Upon complexification, both become the algebra 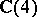. The modified metrics are the metrics of Minkowski space-time (cf. also Minkowski space) and more easily illustrate the physics or the geometry.

In one case (see, for example [a2]) the metric is given by

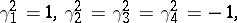the 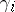generate a 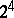-dimensional real Clifford algebra that is isomorphic to , the ring of two-by-two matrices over the real quaternion division ring. Every Clifford algebra 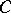admits a -grading,

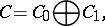such that for all 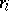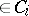and 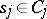, 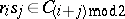. The subspace 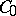, spanned by the identity element and all products of an even number, is, in the present case, a subalgebra isomorphic to to the -dimensional Pauli algebra.

The Majorana representation is the 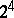-dimensional real Clifford algebra with metric (as in [a1])

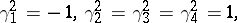that is isomorphic to 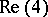. Here, the elements 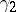, and generate a subalgebra isomorphic to to the -dimensional Pauli algebra.

References

[a1]	E. Cartan, "The theory of spinors" , Dover (1966)
[a2]	E.M. Corson, "Introduction to tensors, spinors, and relativistic wave-equations" , Chelsea (1953)
[a3]	P.A.M. Dirac, "The quantum theory of the electron" Proc. Royal Soc. London , A117 (1928) pp. 610–624
[a4]	N.A. Salingaros, G.P. Wene, "The Clifford algebra of differential forms" Acta Applic. Math. , 4 (1985) pp. 271–191