Algebraic system, automorphism of an

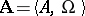An isomorphic mapping of an algebraic system onto itself. An automorphism of an -system is a one-to-one mapping 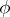of the set 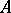onto itself having the following properties:

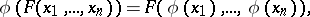(1)

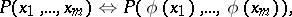(2)

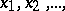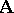for all from and for all from . In other words, an automorphism of an -system is an isomorphic mapping of the system 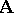onto itself. Let 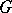be the set of all automorphisms of the system 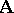. If 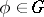, the inverse mapping 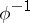also has the properties (1) and (2), and for this reason 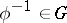. The product 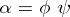of two automorphisms 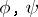of the system 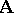, defined by the formula 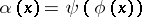, , 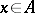is again an automorphism of the system 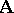. Since multiplication of mappings is associative, 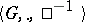is a group, known as the group of all automorphisms of the system 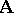; it is denoted by 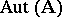. The subgroups of the group 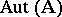are simply called automorphism groups of the system .

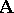Let 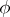be an automorphism of the system 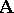and let 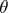be a congruence of this system. Putting

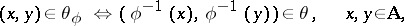one again obtains a congruence 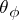of the system 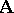. The automorphism 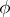is known as an IC-automorphism if 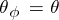for any congruence 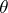of the system 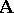. The set 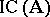of all IC-automorphisms of the system 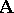is a normal subgroup of the group 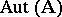, and the quotient group 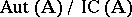is isomorphic to an automorphism group of the lattice of all congruences of the system 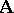[1]. In particular, any inner automorphism 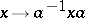of a group defined by a fixed element of this group is an IC-automorphism. However, the example of a cyclic group of prime order shows that not all IC-automorphisms of a group are inner.

Let 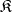be a non-trivial variety of -systems or any other class of -systems comprising free systems of any (non-zero) rank. An automorphism 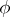of a system 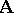of the class 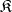is called an I-automorphism if there exists a term 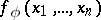of the signature , in the unknowns , for which: 1) in the system 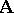there exist elements such that for each element 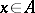the equality

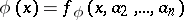is valid; and 2) for any system 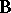of the class 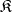the mapping

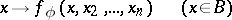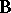is an automorphism of this system for any arbitrary selection of elements in the system . The set 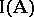of all I-automorphisms for each system 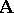of the class 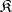is a normal subgroup of the group 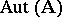. In the class 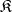of all groups the concept of an I-automorphism coincides with the concept of an inner automorphism of the group [2]. For the more general concept of a formula automorphism of -systems, see [3].

Let 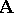be an algebraic system. By replacing each basic operatio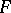n in 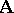by the predicate

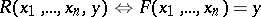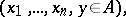one obtains the so-called model 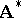which represents the system 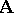. The equality 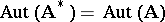is valid. If the systems 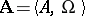and 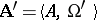have a common carrier 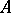, and if 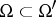, then 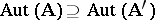. If the -system 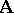with a finite number of generators is finitely approximable, the group 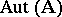is also finitely approximable (cf. [1]). Let 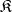be a class of -systems and let 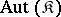be the class of all isomorphic copies of the groups 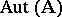, , 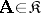and let 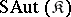be the class of subgroups of groups from the class 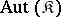. The class 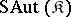consists of groups which are isomorphically imbeddable into the groups , .

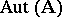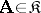The following two problems arose in the study of automorphism groups of algebraic systems.

1) Given a class 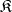of -systems, what can one say about the classes 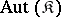and ?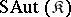

2) Let an (abstract) class 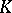of groups be given. Does there exist a class 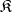of -systems with a given signature such that 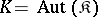or even 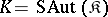? It has been proved that for any axiomatizable class 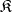of models the class of groups 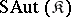is universally axiomatizable [1]. It has also been proved [1], [4] that if 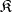is an axiomatizable class of models comprising infinite models, if 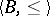is a totally ordered set and if 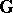is an automorphism group of the model 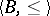, then there exists a model 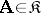such that 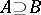, and for each element 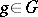there exists an automorphism 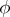of the system 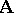such that 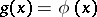for all 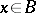. The group 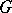is called 1) universal if 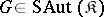for any axiomatizable class 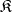of models comprising infinite models; and 2) a group of ordered automorphisms of an ordered group (cf. Totally ordered group) if 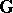is isomorphic to some automorphism group of the group which preserves the given total order 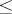of this group (i.e. 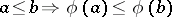for all , ).

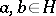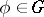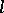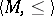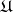Let be the class of totally ordered sets , let be the class of universal groups, let RO be the class of right-ordered groups and let OA be the class of ordered automorphism groups of free Abelian groups. Then [4], [5], [6]:

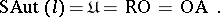Each group is isomorphic to the group of all automorphisms of some -algebra. If 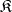is the class of all rings, 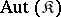is the class of all groups [1]. However, if 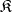is the class of all groups, 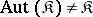; for example, the cyclic groups 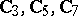of the respective orders 3, 5 and 7 do not belong to the class 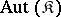. There is also no topological group whose group of all topological automorphisms is isomorphic to 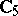[7].

References

[1]	B.I. Plotkin, "Groups of automorphisms of algebraic systems" , Wolters-Noordhoff (1972)
[2]	B. Csákány, "Inner automorphisms of universal algebras" Publ. Math. Debrecen , 12 (1965) pp. 331–333
[3]	J. Grant, "Automorphisms definable by formulas" Pacific J. Math. , 44 (1973) pp. 107–115
[4]	M.O. Rabin, "Universal groups of automorphisms of models" , Theory of models , North-Holland (1965) pp. 274–284
[5]	P.M. Cohn, "Groups of order automorphisms of ordered sets" Mathematika , 4 (1957) pp. 41–50
[6]	D.M. Smirnov, "Right-ordered groups" Algebra i Logika , 5 : 6 (1966) pp. 41–59 (In Russian)
[7]	R.J. Wille, "The existence of a topological group with automorphism group 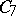" Quart. J. Math. Oxford (2) , 18 (1967) pp. 53–57