Relative homology
From Encyclopedia of Mathematics
The homology groups (cf. Homology group) 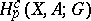 of a pair of spaces
of a pair of spaces 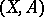 . They are defined by the quotient complex of the chain complex
. They are defined by the quotient complex of the chain complex 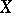 with coefficients in a group
with coefficients in a group 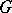 by the subcomplex consisting of all chains with support in
by the subcomplex consisting of all chains with support in 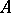 . These groups are usually not altered by "excisionexcision" , i.e. by the replacement of the pair
. These groups are usually not altered by "excisionexcision" , i.e. by the replacement of the pair 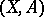 by a pair
by a pair  , where
, where 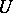 is an open subset of
is an open subset of 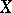 contained in
contained in 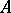 . The relative cohomology groups
. The relative cohomology groups 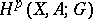 are defined by the subcomplex of the chain complex
are defined by the subcomplex of the chain complex 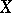 consisting of all cochains with support in
consisting of all cochains with support in 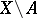 , while the quotient complex usually defines cohomology groups of the subset
, while the quotient complex usually defines cohomology groups of the subset  .
.
References
| [1] | E.G. Sklyarenko, "Homology and cohomology of general spaces" , Springer (Forthcoming) (Translated from Russian) |
Comments
References
| [a1] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) |
| [a2] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. 360ff |
How to Cite This Entry:
Relative homology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relative_homology&oldid=13630
Relative homology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Relative_homology&oldid=13630
This article was adapted from an original article by E.G. Sklyarenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article