Jacobi transform

The integral transforms

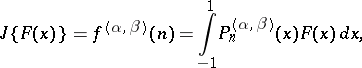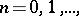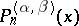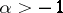where the are the Jacobi polynomials of degree , and and are real numbers. The inversion formula has the form

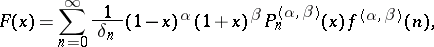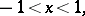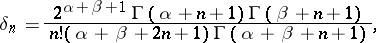provided the series converges.

The Jacobi transform reduces the operation

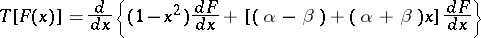to an algebraic one by the formula

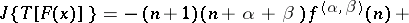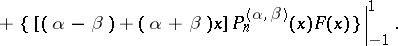When 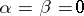the Jacobi transform is the Legendre transform; for 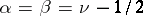it is the Gegenbauer transform. Jacobi transforms are used in solving differential equations containing the operator 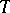. The Jacobi transform has also been defined for a special class of generalized functions.

References

[1]	E.J. Scott, "Jacobi transforms" Quart. J. Math. , 4 : 13 (1953) pp. 36–40
[2]	V.A. Ditkin, A.P. Prundnikov, "Integral transforms" Progress in Math. (1969) pp. 1–85 Itogi Nauk. Mat. Anal. 1966 (1967)
[3]	A.G. Zemanian, "Generalized integral transformations" , Interscience (1968)

Comments

See (the editorial comments to) Gegenbauer transform. Usually the Jacobi transform is written as

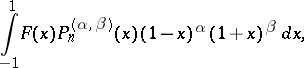which generalizes the expression given in Gegenbauer transform.