Weingarten derivational formulas

Formulas yielding the expansion of the derivative of the unit normal vector to a surface in terms of the first derivatives of the position vector of this surface. Let be the position vector of the surface, let 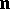be the unit normal vector and let 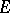, , , , 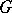, 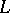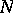be the coefficients of the first and second fundamental forms of the surface, respectively; the Weingarten derivational formulas will then take the form

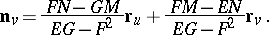The formulas were established in 1861 by J. Weingarten.

References

[1]	P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)

References

[a1]	W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973)
[a2]	N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965)