Quantum sphere

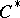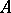A -algebra generated by two elements and 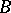satisfying [a1]

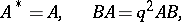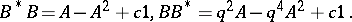Here, is a deformation parameter and 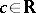is another parameter labeling the family of quantum spheres. Each quantum sphere is a quantum homogeneous space in the sense that there exists a right co-action

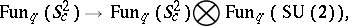where 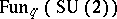stands for the quantum group 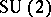[a7] (cf. also Quantum groups) considered as a deformation of the Poisson algebra 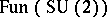. The one-parameter family of quantum spheres is in correspondence with the family of 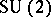-covariant Poisson structures on 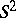, which is known to be one-parametric too ([a2], Appendix). The deformation of the Poisson structure 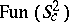can be introduced in a precisely defined manner [a2]. Also, the structure of representations of 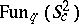is in correspondence with the structure of symplectic leaves on [a1], [a2]. For , the symplectic leaves are two open discs and the points of a circle separating them. For , one disc leaf is attached to one one-point leaf and, in fact, this is the Bruhat decomposition of the Poisson homogeneous space . For 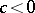, is a symplectic manifold.

The symplectic spheres 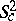, with 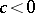, can be realized as orbits of the dressing transformation of 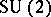acting on its dual Poisson Lie group. An equivalent realization is given by the right 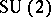-action on the manifold 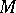of unimodular positive matrices, which is just the unitary transformation 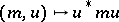. There exists a quantum analogue as a right co-action , which is defined formally in the same way as in the Poisson case. If 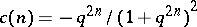, , 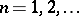one can construct, using this structure, the -dimensional irreducible representation of the deformed universal enveloping algebra 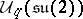[a3]. Moreover, if 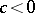, then the 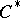-algebra 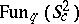is non-trivial only for 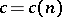[a1].

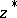A few other concepts have been developed for quantum spheres, including a description in terms of a local holomorphic coordinate and its adjoint [a3], [a4] and a differential and integral calculus [a4], [a5]. In a precise analogy with the classical case, quantum spherical functions were defined as special basis elements in

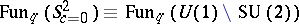and expressed in terms of big -Jacobi polynomials [a6].

References

[a1]	P. Podles, "Quantum spheres" Lett. Math. Phys. , 14 (1987) pp. 193–202
[a2]	A.J.L. Sheu, "Quantization of the Poisson and its Poisson homogeneous space — the -sphere" Comm. Math. Phys. , 135 (1991) pp. 217–232
[a3]	P. Šťovíček, "Quantum line bundles on 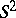and the method of orbits for " J. Math. Phys. , 34 (1993) pp. 1606–1613
[a4]	C.S. Chu, P.M. Ho, B. Zumino, "The quantum -sphere as a complex manifold" Z. Phys. C , 70 (1996) pp. 339–344
[a5]	P. Podles, "Differential calculus on quantum spheres" Lett. Math. Phys. , 18 (1989) pp. 107–119
[a6]	M. Noumi, K. Mimachi, "Quantum -spheres and big 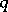-Jacobi polynomials" Comm. Math. Phys. , 128 (1990) pp. 521–531
[a7]	S.L. Woronowicz, "Twisted 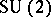group. An example of a non-commutative differential calculus" Publ. RIMS Univ. Kyoto , 23 (1987) pp. 117–181