Fermat principle
A variational principle that enables one to find rays, that is, curves, along which a wave process propagates. Let 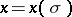 ,
, 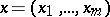 ,
, 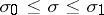 , be the equation of a curve
, be the equation of a curve 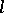 joining two points
joining two points 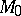 and
and 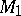 , and let
, and let 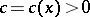 be the velocity of wave propagation at
be the velocity of wave propagation at  . The Fermat principle asserts that
. The Fermat principle asserts that 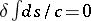 for the ray joining
for the ray joining 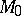 and
and 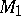 . Here
. Here 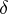 is the variation symbol, and
is the variation symbol, and 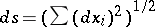 is the arc differential. The physical meaning of
is the arc differential. The physical meaning of 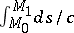 is the time of motion from
is the time of motion from 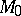 to
to 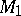 along
along 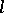 with velocity
with velocity 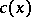 . The Fermat principle implies the classical laws of reflection, refraction and straightness of rays for
. The Fermat principle implies the classical laws of reflection, refraction and straightness of rays for 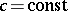 . Diffraction rays, rays propagated from the edges of screens, and rays of leading waves can also be found using the Fermat principle. Rays determined by the Fermat principle are characteristics of the eikonal equation. The integral
. Diffraction rays, rays propagated from the edges of screens, and rays of leading waves can also be found using the Fermat principle. Rays determined by the Fermat principle are characteristics of the eikonal equation. The integral 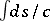 gives a Riemannian metric of a particular type. The rays are the geodesics corresponding to this metric. The Fermat principle can be generalized to the case of a velocity depending on the direction (an anisotropic medium). The rays in this case are the geodesics of some Finsler metric.
gives a Riemannian metric of a particular type. The rays are the geodesics corresponding to this metric. The Fermat principle can be generalized to the case of a velocity depending on the direction (an anisotropic medium). The rays in this case are the geodesics of some Finsler metric.
The Fermat principle for the problem of the refraction of light was first stated by P. Fermat in about 1660.
For references see Ray method.
Fermat principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat_principle&oldid=13288