Closure space
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
Let  be a set and
be a set and  the set of subsets of
the set of subsets of  . A function
. A function  is a closure operation if for all
is a closure operation if for all  :
:
K1)  ;
;
K2)  ;
;
K3)  ;
;
K4)  ;
;
K5)  . These are the Kuratowski closure axioms, and a function
. These are the Kuratowski closure axioms, and a function  satisfying these axioms is called a Kuratowski closure operator (or Kuratowski closure operation).
satisfying these axioms is called a Kuratowski closure operator (or Kuratowski closure operation).
A pair 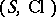 is a closure space if and only if
is a closure space if and only if  satisfies:
satisfies:
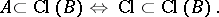 |
This condition is equivalent to K1)–K3). A closure space that satisfies K5) is a Fréchet  -space. A Fréchet
-space. A Fréchet  -space that satisfies K4) is a topological space.
-space that satisfies K4) is a topological space.
A Čech closure operator is a mapping 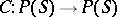 such that
such that
C1)  ;
;
C2) ( K1))
K1))  ;
;
C3)  . A set endowed with a Čech closure operator is called a pre-topological space.
. A set endowed with a Čech closure operator is called a pre-topological space.
References
| [a1] | N.M. Martin, S. Pollard, "Closure spaces and logic" , Kluwer Acad. Publ. (1996) |
| [a2] | J.L. Kelley, "General topology" , v. Nostrand–Reinhold (1955) |
| [a3] | D. Dikranjan, W. Tholin, "Categorical structures of closure operators" , Kluwer Acad. Publ. (1996) |
How to Cite This Entry:
Closure space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closure_space&oldid=13257
Closure space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closure_space&oldid=13257
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article