Charlier polynomials
From Encyclopedia of Mathematics
Polynomials that are orthogonal on the system of non-negative integer points with an integral weight 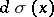 , where
, where  is a step function with jumps defined by the formula
is a step function with jumps defined by the formula
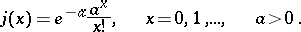 |
The orthonormal Charlier polynomials have the following representations:
 |
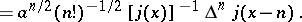 |
The Charlier polynomials are connected with the Laguerre polynomials by
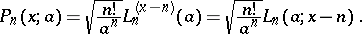 |
Introduced by C. Charlier [1]. Since the function 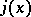 defines a Poisson distribution, the polynomials
defines a Poisson distribution, the polynomials 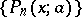 are called Charlier–Poisson polynomials.
are called Charlier–Poisson polynomials.
References
| [1] | C. Charlier, "Application de la théorie des probabilités à l'astronomie" , Paris (1931) |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [3] | G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975) |
Comments
In the formula above,  denotes taking first differences, i.e.
denotes taking first differences, i.e. 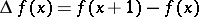 . Another common notation and an expression by hypergeometric functions is:
. Another common notation and an expression by hypergeometric functions is:
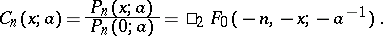 |
How to Cite This Entry:
Charlier polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Charlier_polynomials&oldid=13248
Charlier polynomials. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Charlier_polynomials&oldid=13248
This article was adapted from an original article by P.K. Suetin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article