Semi-symplectic space

A projective 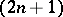-space in which there is given a 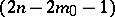-plane 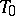, in this a 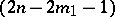-plane 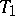, etc., up to a 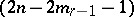-plane 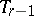, where in the space a null-system is given, taking all the points of the space to planes passing through the plane 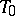; the plane 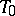is given an absolute null-system taking all its points to 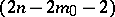-planes lying in it and passing through the 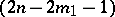-plane 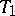, etc., up to an absolute null-system of the 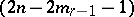-plane 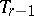, taking all its points to 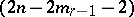-planes lying in it, 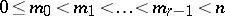. This semi-symplectic space is denoted by .

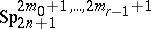A semi-symplectic space is obtained by a method analogous to the transition from elliptic and hyperbolic spaces to semi-elliptic and semi-hyperbolic spaces, and is more general than a quasi-symplectic space.

The collineations of a semi-symplectic space that take the planes 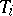to themselves and that commute with the null-systems are called semi-symplectic transformations of the semi-symplectic space.

There exist invariants of semi-symplectic transformations analogous to the symplectic invariants of symplectic spaces. The semi-symplectic transformations form a Lie group.

References

[1]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)

References

[a1]	B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian)