Conjugate trigonometric series

to the series

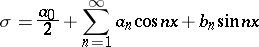The series

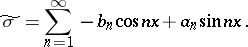These series are the real and imaginary parts, respectively, of the series

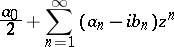where . The formula for the partial sums of the trigonometric series conjugate to the Fourier series of 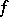is

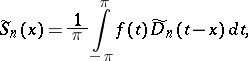where 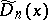is the conjugate Dirichlet kernel. If 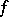is a function of bounded variation on 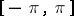, then a necessary and sufficient condition for the convergence of at a point 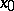is the existence of the conjugate function (see Conjugate function Section 3) 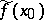, and this is then the sum of the series 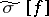. If 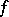is a summable function on 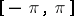, then can be summed almost-everywhere by the method 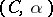, , 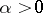and by the Abel–Poisson method, and the sum coincides almost-everywhere with the conjugate o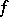f . If 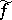is summable, then the conjugate series 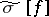is its Fourier series. The function 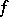need not be summable; in the case of generalizations of the Lebesgue integral such as the 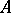-integral and the Boks integral, the conjugate series 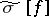is always the Fourier series of the conjugate function.

References

[1]	A. Tauber, "Ueber den Zusammenhang des reellen und imaginären Teiles einer Potenzreihe" Monatsh. Math. Phys. , 2 (1891) pp. 79–118
[2]	W.H. Young, Sitzungsber. Bayer. Akad. Wiss. München Math. Nat. Kl. , 41 (1911) pp. 361–371
[3]	I.I. [I.I. Privalov] Priwalow, "Sur les fonctions conjuguées" Bull. Soc. Math. France , 44 (1916) pp. 100–103
[4]	I.I. Privalov, "The Cauchy integral" , Saratov (1919) pp. 61–104 (In Russian)
[5]	N.N. Luzin, "The integral and trigonometric series" , Moscow-Leningrad (1951) (In Russian) (Thesis; also: Collected Works, Vol. 1, Moscow, 1953, pp. 48–212)
[6]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Oxford Univ. Press (1964) (Translated from Russian)
[7]	I.A. Vinogradova, "Generalized integrals and Fourier series" Itogi Nauk. Mat. Anal. 1970 (1971) pp. 65–107 (In Russian)
[8]	L.V. Zhizhiashvili, "Conjugate functions and trigonometric series" , Tbilisi (1969) (In Russian)

Comments

Reference [7] is a long useful survey. The references [a1], [a2] are standard.

References

[a1]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1959–1968)
[a2]	G.H. Hardy, W.W. Rogosinsky, "Fourier series" , Cambridge Univ. Press (1950)