Isothermal coordinates

Coordinates of a two-dimensional Riemannian space in which the square of the line element has the form:

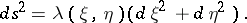Isothermal coordinates specify a conformal mapping of the two-dimensional Riemannian manifold into the Euclidean plane. Isothermal coordinates can always be introduced in a compact domain of a regular two-dimensional manifold. The Gaussian curvature can be calculated in isothermal coordinates by the formula:

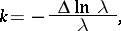where is the Laplace operator.

Isothermal coordinates are also considered in two-dimensional pseudo-Riemannian spaces; the square of the line element then has the form:

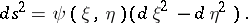Here, frequent use is made of coordinates which are naturally connected with isothermal coordinates and in which the square of the line element has the form:

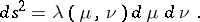In this case the lines and are isotropic geodesics and the coordinate system is called isotropic. Isotropic coordinates are extensively used in general relativity theory.

References

[a1]	W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973)