Perimeter

The perimeter of a planar region bounded by a rectifiable curve is the total length of the boundary of this region.

The perimeter of a measurable set 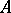in an -dimensional Euclidean (or Riemannian) space is the lower limit of the 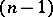-dimensional areas of boundaries of polyhedra 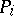(or sets 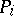with 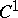-smooth boundaries) converging to 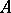in volume, i.e. such that 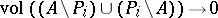as .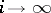

References

[1a]	R. Caccoppoli, "Misura e integrazione sugli insiemi dimensionalmente orientati I" Rend. Accad. Naz. Lincei Ser. 8 , 12 : 1 (1952) pp. 3–11
[1b]	R. Caccoppoli, "Misura e integrazione sugli insiemi dimensionalmente orientati II" Rend. Accad. Naz. Lincei Ser. 8 , 12 : 2 (1952) pp. 137–146
[2]	E. de Giorgi, "Sulla proprietà isoperimetrica dell'ipersfera, nella classe degli insiemi aventi frontiera orientata di misura finita" Rend. Accad. Naz. Lincei Ser. 1 , 5 : 2 (1958) pp. 33–34

References

[a1]	E. Giusti, "Minimal surfaces and functions of bounded variation" , Birkhäuser (1984)
[a2]	M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French)
[a3]	Yu.D. Burago, V.A. Zalgaller, "Geometric inequalities" , Springer (1988) (Translated from Russian)
[a4]	H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108