Invariance, principle of
Let 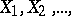 be independent identically-distributed real-valued random variables with zero expectation and variance
be independent identically-distributed real-valued random variables with zero expectation and variance 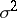 ; consider the random polygonal line
; consider the random polygonal line
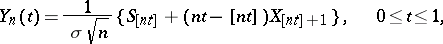 |
where 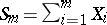 . If
. If 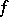 is a real-valued continuous function on the space
is a real-valued continuous function on the space 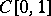 of continuous functions on
of continuous functions on 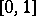 with the supremum norm (or only continuous everywhere except on a set of Wiener measure zero), then
with the supremum norm (or only continuous everywhere except on a set of Wiener measure zero), then 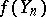 converges in distribution to
converges in distribution to 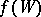 , where
, where  is a Wiener random function. Thus, the limiting distribution for the
is a Wiener random function. Thus, the limiting distribution for the 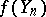 does not depend on any special properties of the
does not depend on any special properties of the 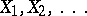 .
.
A typical scheme for the use of the invariance principle consists in finding the limiting distribution for the  by finding the limiting distribution for
by finding the limiting distribution for 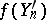 , where
, where 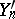 is a random polygonal line constructed in the same way as
is a random polygonal line constructed in the same way as 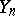 from some specially chosen sequence
from some specially chosen sequence 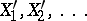 . For example, if
. For example, if
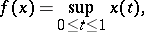 |
then 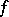 is continuous on
is continuous on 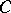 , and, since
, and, since
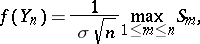 |
one has that
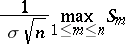 |
converges in distribution to 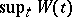 . To find the distribution of
. To find the distribution of 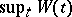 , the sequence
, the sequence 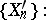
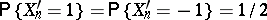 is used, and as a result of the calculations one obtains
is used, and as a result of the calculations one obtains
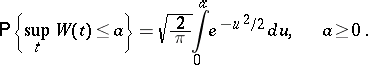 |
References
| [1] | M. Donsker, "An invariance principle for certain probability limit theorems" Memoirs Amer. Math. Soc. , 6 (1951) pp. 1–12 |
| [2] | Yu.V. Prokhorov, "Convergence of random processes and limit theorems in probability theory" Theor. Probab. Appl. , 1 (1956) pp. 157–214 Teor. Veroyatnost. Prilozhen. , 1 : 2 (1956) pp. 177–238 |
| [3] | P. Billingsley, "Convergence of probability measures" , Wiley (1968) |
Comments
References
| [a1] | L.P. Breiman, "Probability" , Addison-Wesley (1968) |
Invariance, principle of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Invariance,_principle_of&oldid=13150