Conjunctive normal form
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A propositional formula of the form
 | (*) |
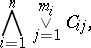where each 
, 
; 
, is either an atomic formula (a variable or constant) or the negation of an atomic formula. The conjunctive normal form (*) is a tautology if and only if for any 
one can find both formulas 
and 
among the 
, for some atomic formula 
. Given any propositional formula 
, one can construct a conjunctive normal form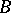 
equivalent to it and containing the same variables and constants as 
. This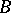 
is called the conjunctive normal form of 
.
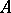Comments
The dual of a conjunctive normal form is a disjunctive normal form. Both are also used in the theory of Boolean functions (cf. Boolean functions, normal forms of).
How to Cite This Entry:
Conjunctive normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjunctive_normal_form&oldid=13117
Conjunctive normal form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjunctive_normal_form&oldid=13117
This article was adapted from an original article by S.K. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article