Extremal length
of a family of curves
A concept which, along with that of the modulus of a family of curves, is a general form of the definition of conformal invariants and lies at the basis of the method of the extremal metric (cf. Extremal metric, method of the).
Let 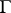 be a family of locally rectifiable curves on a Riemann surface
be a family of locally rectifiable curves on a Riemann surface 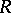 . The modulus problem is defined for
. The modulus problem is defined for 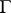 if there is a non-empty class
if there is a non-empty class 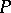 of conformally-invariant metrics (cf. Conformally-invariant metric)
of conformally-invariant metrics (cf. Conformally-invariant metric) 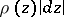 given on
given on 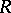 such that
such that 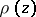 is square integrable in the
is square integrable in the  -plane for every local uniformizing parameter
-plane for every local uniformizing parameter 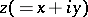 and if
and if
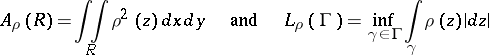 |
are not simultaneously equal to  or
or 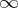 . (Each of the above integrals is understood as a Lebesgue integral.) In this case the quantity
. (Each of the above integrals is understood as a Lebesgue integral.) In this case the quantity
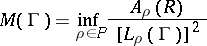 |
is called the modulus of the family of curves  . The reciprocal of
. The reciprocal of 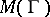 is called the extremal length of the family of curves
is called the extremal length of the family of curves 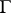 .
.
The modulus problem for a family of curves is often defined as follows: Let 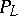 be the subclass of
be the subclass of 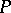 such that for
such that for 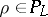 and
and 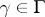 ,
,
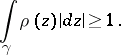 |
If the set 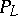 is non-empty, then the quantity
is non-empty, then the quantity
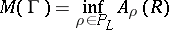 |
is called the modulus of the family 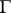 . If
. If 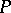 is non-empty but
is non-empty but 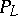 is empty, then
is empty, then 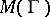 is assigned the value
is assigned the value 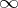 . It is the latter definition of the modulus that is adopted below.
. It is the latter definition of the modulus that is adopted below.
Let 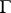 be a family of locally rectifiable curves on a Riemann surface
be a family of locally rectifiable curves on a Riemann surface 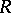 for which the modulus problem is defined, and let
for which the modulus problem is defined, and let 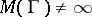 . Then every metric from
. Then every metric from 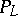 is an admissible metric for the modulus problem for
is an admissible metric for the modulus problem for 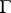 . If in
. If in 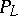 there is a metric
there is a metric 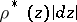 for which
for which
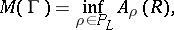 |
then this metric is called an extremal metric in the modulus problem for 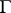 .
.
The fundamental property of the modulus is its conformal invariance.
Theorem 1. Let 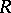 and
and 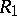 be two conformally-equivalent Riemann surfaces, let
be two conformally-equivalent Riemann surfaces, let 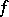 be a univalent conformal mapping of
be a univalent conformal mapping of 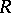 onto
onto 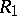 , let
, let 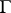 be a family of locally rectifiable curves given on
be a family of locally rectifiable curves given on 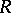 , and let
, and let 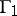 be the family of images of the curves in
be the family of images of the curves in  under
under 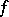 . If the modulus problem is defined for
. If the modulus problem is defined for 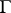 and the modulus of
and the modulus of 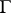 is
is 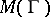 , then the modulus problem is also defined for
, then the modulus problem is also defined for 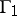 and
and 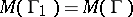 .
.
The following theorem shows that if there is an extremal metric, then it is essentially unique:
Theorem 2. Let  be a family of locally rectifiable curves on a Riemann surface
be a family of locally rectifiable curves on a Riemann surface 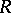 , and suppose that the modulus problem is defined for
, and suppose that the modulus problem is defined for 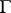 and that
and that 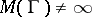 . If
. If 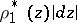 and
and 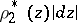 are extremal metrics for this modulus problem, then
are extremal metrics for this modulus problem, then 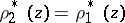 everywhere on
everywhere on 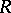 except, possibly, on a subset of
except, possibly, on a subset of 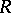 of measure zero.
of measure zero.
Examples of moduli of families of curves.
1) Let 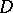 be a rectangle with sides
be a rectangle with sides  and
and 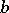 , and let
, and let 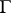 (
(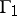 ) be a family of locally rectifiable curves in
) be a family of locally rectifiable curves in 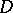 that join the sides of length
that join the sides of length  (
(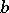 ). Then
). Then
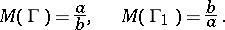 |
2) Let 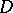 be the annulus
be the annulus 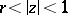 , let
, let 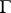 be the class of rectifiable Jordan curves in
be the class of rectifiable Jordan curves in 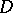 that separate the boundary components of
that separate the boundary components of 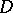 and let
and let 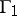 be the class of locally rectifiable curves in
be the class of locally rectifiable curves in 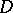 that join the boundary components of
that join the boundary components of 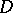 . Then
. Then 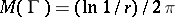 and
and 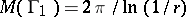 . In both cases
. In both cases 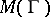 and
and 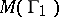 are characteristic conformal invariants of
are characteristic conformal invariants of 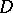 . Hence,
. Hence, 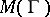 is called the modulus of the domain
is called the modulus of the domain 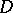 for the class
for the class 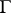 and
and 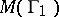 is called the modulus of
is called the modulus of 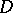 for
for 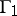 .
.
There is a well-known connection between the moduli of families of curves under a quasi-conformal mapping. Let 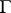 be a family of curves in some domain
be a family of curves in some domain 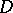 and let
and let 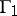 be the image of
be the image of 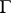 under a
under a 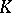 -quasi-conformal mapping of
-quasi-conformal mapping of 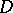 . Then the moduli
. Then the moduli 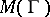 and
and 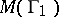 of
of 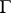 and
and 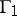 , respectively, satisfy the inequality
, respectively, satisfy the inequality
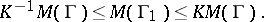 |
The generalization of the concept of the modulus to several families of curves turns out to be important in applications. Let 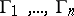 be families of locally rectifiable curves on a Riemann surface
be families of locally rectifiable curves on a Riemann surface 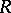 (as a rule,
(as a rule, 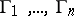 are, respectively, homotopy classes of curves). Let
are, respectively, homotopy classes of curves). Let  be non-negative real numbers, not all equal to zero, and let
be non-negative real numbers, not all equal to zero, and let 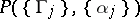 be the class of conformally-invariant metrics
be the class of conformally-invariant metrics 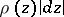 on
on 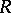 for which
for which 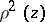 is integrable for every local parameter
is integrable for every local parameter 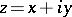 and such that
and such that
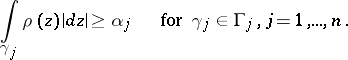 |
If the set 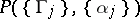 is non-empty, then the modulus problem
is non-empty, then the modulus problem 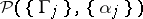 is said to be defined for the families of curves
is said to be defined for the families of curves 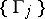 and the numbers
and the numbers 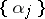 . In this case the quantity
. In this case the quantity
 |
is called the modulus of this problem. If in 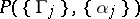 there is a metric
there is a metric 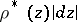 for which
for which
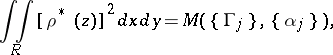 |
then this metric is called an extremal metric for the modulus problem 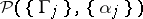 .
.
The modulus problem defined in this way is also a conformal invariant. For such moduli a uniqueness theorem analogous to Theorem 2 holds. The existence of an extremal metric for the modulus problem 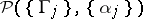 has been proved under fairly general assumptions. The above definition extends to the case of families of curves
has been proved under fairly general assumptions. The above definition extends to the case of families of curves 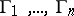 on a surface
on a surface 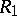 obtained by removing from
obtained by removing from 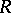 finitely many points
finitely many points 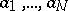 , where the families
, where the families 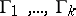 ,
, 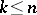 , consist of closed Jordan curves homotopic on
, consist of closed Jordan curves homotopic on 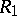 to circles of sufficiently small radii and centres at corresponding selected points. Such an extremal-metric problem in conjunction with the above concept of the modulus of a simply-connected domain
to circles of sufficiently small radii and centres at corresponding selected points. Such an extremal-metric problem in conjunction with the above concept of the modulus of a simply-connected domain 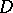 relative to a point
relative to a point 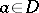 (see Modulus of an annulus) is connected with the theory of capacity of plane sets.
(see Modulus of an annulus) is connected with the theory of capacity of plane sets.
Other generalizations and modifications of the concept of the modulus of a family of curves are also known (see [6]–[10]). This concept has been extended to the case of curves and surfaces in space. Uniqueness theorems and a number of properties of such moduli have been established, in particular, an analogue of the inequalities
for 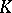 -quasi-conformal mappings in space has been obtained (see [9] and [10]).
-quasi-conformal mappings in space has been obtained (see [9] and [10]).
References
| [1] | L.V. Ahlfors, A. Beurling, "Conformal invariants and function-theoretic null-sets" Acta Math. , 83 (1950) pp. 101–129 |
| [2] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
| [3] | L.V. Ahlfors, "Lectures on quasiconformal mappings" , v. Nostrand (1966) |
| [4] | J.A. Jenkins, "On the existence of certain general extremal metrics" Ann. of Math. , 66 : 3 (1957) pp. 440–453 |
| [5] | G.V. Kuz'mina, "Moduli of families of curves and quadratic differentials" , Amer. Math. Soc. (1982) (Translated from Russian) |
| [6] | J. Hersch, "Longeurs extrémales et théorie des fonctions" Comment. Math. Helv. , 29 : 4 (1955) pp. 301–337 |
| [7] | P.M. Tamrazov, "A theorem of line integrals for extremal length" Dokl. Akad. Nauk Ukrain. SSSR , 1 (1966) pp. 51–54 ((in Ukrainian; English summary)) |
| [8] | B. Fuglede, "Extremal length and functional completion" Acta Math. , 98 (1957) pp. 171–219 |
| [9] | B.V. Shabat, "The modulus method in space" Soviet Math. Dokl. , 1 : 1 (1960) pp. 165–168 Dokl. Akad. Nauk SSSR , 130 : 6 (1960) pp. 1210–1213 |
| [10] | A.V. Sychev, "Moduli and quasi-conformal mappings in space" , Novosibirsk (1983) (In Russian) |
Extremal length. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extremal_length&oldid=13112